
分析 由于q为无穷等比数列{an}的公比,即有0<|q|<1,由无穷等比数列的极限公式可得$\underset{lim}{n→∞}$(a3+a4+…+an)=$\frac{{a}_{3}}{1-q}$,再由等比数列的通项公式,解方程可得公比q.
解答 解:由于q为无穷等比数列{an}的公比,即有0<|q|<1,
由${a_1}=\lim_{n→∞}({a_3}+{a_4}+…+{a_n})$,可得
a1=$\frac{{a}_{3}}{1-q}$=$\frac{{a}_{1}{q}^{2}}{1-q}$,
即为q2+q-1=0,
解得q=$\frac{\sqrt{5}-1}{2}$($\frac{-1-\sqrt{5}}{2}$舍去),
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查数列的极限的求法,注意运用无穷等比数列的极限公式,考查运算能力,属于中档题.


科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(理)试卷(解析版) 题型:解答题
公园里有一扇形湖面,管理部门打算在湖中建一三角形观景平台,希望面积与周长都最大.如图所示扇形 ,圆心角
,圆心角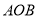 的大小等于
的大小等于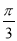 ,半径为
,半径为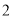 百米,在半径
百米,在半径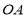 上取一点
上取一点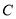 ,过点
,过点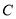 作平行于
作平行于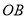 的直线交弧
的直线交弧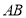 于点
于点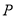 .设
.设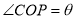 .
.
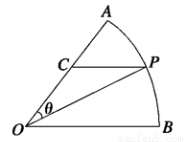
(1)求△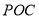 面积
面积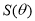 的函数表达式.
的函数表达式.
(2)求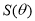 的最大值及此时
的最大值及此时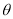 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | [-2,-1)∪(-1,1)∪(1,2] | C. | (-∞,-2)∪(2,+∞) | D. | [-2,-1)∪(1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com