
分析 (1)根据椭圆的定义可求出轨迹方程;
(2)设P(cosα,$\sqrt{2}$sinα),代入距离公式,利用二次函数的性质求出d(a);
(3)分别表示出S1及S2,由正数m满足S1≤mS2得出m2≥$\frac{{{a}^{2}-a}^{4}}{8({a}^{2}+1)^{2}}$,利用换元法和二次函数的性质得出右侧式子的最大值即可求出m的最小值.
解答 解:(1)设动圆的圆心坐标为C(x,y),则动圆的半径r=|CF|
圆E的圆心为E(0,-1),半径为2$\sqrt{2}$,
∵动圆与圆E内切,∴|CE|+|CF|=2$\sqrt{2}$,
∴动圆C的圆心轨迹为以E,F为焦点的椭圆,
设此椭圆方程为$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$,
则$\left\{\begin{array}{l}{{a}^{2}-{b}^{2}={c}^{2}}\\{c=1}\\{2a=2\sqrt{2}}\end{array}\right.$,解得a=$\sqrt{2}$,b=1.
∴动圆的圆心的轨迹方程为$\frac{{y}^{2}}{2}+{x}^{2}$=1.
(2)设P(cosα,$\sqrt{2}$sinα),则|PA|2=(cosα-a)2+2sin2α
=-cos2α-2acosα+a2+2=-(cosα+a)2+2a2+2
①若-1≤a≤1,则当cosα=-a时,|PA|2取得最大值2a2+2,∴d(a)=$\sqrt{2{a}^{2}+2}$,
②若-a≤-1,即a≥1,则当cosα=-1时,|PA|2取得最大值-(a-1)2+2a2+2=a2+2a+1=(a+1)2,
∴d(a)=$\sqrt{(a+1)^{2}}$=|a+1|=a+1;
③若-a≥1,即a≤-1,则当cosα=1时,|PA|2取得最大值-(a+1)2+2a2+2=a2-2a+1=(a-1)2,
∴d(a)=$\sqrt{(a-1)^{2}}$=|a-1|=1-a.
综上,d(a)=$\left\{\begin{array}{l}{\sqrt{2{a}^{2}+2},-1≤a≤1}\\{a+1,a>1}\\{1-a,a<1}\end{array}\right.$.
(3)把x=a代入$\frac{{y}^{2}}{2}+{x}^{2}$=1得y=±$\sqrt{2-{2a}^{2}}$,∴不妨设P(a,$\sqrt{2-2{a}^{2}}$),
则S1=S△POA=$\frac{1}{2}×a×\sqrt{2-2{a}^{2}}$,
由(2)可知d(a)=$\sqrt{2{a}^{2}+2}$,∴S2=d2(a)=2a2+2,
∵S1≤mS2,∴m≥$\frac{{S}_{1}}{{S}_{2}}$=$\frac{a\sqrt{2-2{a}^{2}}}{4({a}^{2}+1)}$,
∴m2≥$\frac{{{a}^{2}-a}^{4}}{8({a}^{2}+1)^{2}}$,令f(a)=$\frac{{{a}^{2}-a}^{4}}{8({a}^{2}+1)^{2}}$,a2+1=t,
则f(a)=$\frac{t-1-(t-1)^{2}}{8{t}^{2}}$=-$\frac{1}{4}$($\frac{1}{t}$-$\frac{3}{4}$)2+$\frac{1}{64}$.
∵0≤a≤1,∴1≤t≤2,∴$\frac{1}{2}$≤$\frac{1}{t}$≤1.
∴当$\frac{1}{t}=\frac{3}{4}$时,f(a)取得最大值$\frac{1}{64}$.即m2≥$\frac{1}{64}$.
∴m≥$\frac{1}{8}$,∴m的最小值为$\frac{1}{8}$.
点评 本题考查了椭圆的定义,两点间的距离公式、二次函数的单调性、换元法、分类讨论的思想方法是解题的关键.


科目:高中数学 来源: 题型:选择题
 我们通常把圆、椭圆、抛物线、双曲线统称为圆锥曲线.通过普通高中课程实验教科书《数学》2-1第二章《圆锥曲线与方程》章头引言我们知道,用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.实际上,设圆锥母线与轴所成角为α,不过圆锥顶点的截面与轴所成角为θ.当θ=$\frac{π}{2}$,截口曲线为圆,当$α<θ<\frac{π}{2}$时,截口曲线为椭圆;当0≤θ<α时,截口曲线为双曲线; 当θ=α时,截口曲线为抛物线;如图2,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
我们通常把圆、椭圆、抛物线、双曲线统称为圆锥曲线.通过普通高中课程实验教科书《数学》2-1第二章《圆锥曲线与方程》章头引言我们知道,用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.实际上,设圆锥母线与轴所成角为α,不过圆锥顶点的截面与轴所成角为θ.当θ=$\frac{π}{2}$,截口曲线为圆,当$α<θ<\frac{π}{2}$时,截口曲线为椭圆;当0≤θ<α时,截口曲线为双曲线; 当θ=α时,截口曲线为抛物线;如图2,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )| A. | 一段双曲线弧 | B. | 一段椭圆弧 | C. | 一段圆弧 | D. | 一段抛物线弧 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,三棱锥的四个顶点P、A、B、C在同一个球面上,顶点P在平面ABC内的射影是H,若球心在直线PH上,则点H一定是△ABC的( )
如图,三棱锥的四个顶点P、A、B、C在同一个球面上,顶点P在平面ABC内的射影是H,若球心在直线PH上,则点H一定是△ABC的( )| A. | 重心 | B. | 垂心 | C. | 内心 | D. | 外心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
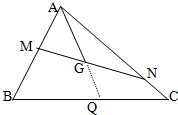 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )| A. | 2 | B. | $\frac{1}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 12 | C. | 9 | D. | 与k的取值有关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com