
分析 根据向量模的计算和向量的数量积公式即可求出答案.
解答 解:∵$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,|$\overrightarrow{{e}_{1}}$|=1,|$\overrightarrow{{e}_{2}}$|=2,
∴|$\overrightarrow{a}$|2=(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)2=4$\overrightarrow{{e}_{1}}$2+$\overrightarrow{{e}_{2}}$2+4$\overrightarrow{{e}_{1}}$$\overrightarrow{{e}_{2}}$=4|$\overrightarrow{{e}_{1}}$|2+|$\overrightarrow{{e}_{2}}$|2+4|$\overrightarrow{{e}_{1}}$|•|$\overrightarrow{{e}_{2}}$|cos120°=4+4-4=4,
∴|$\overrightarrow{a}$|=2,
故答案为:2.
点评 本题考查了向量模的计算和向量的数量积的运算,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=xsinx | B. | y=x2cosx | C. | y=$\frac{sinx}{x}$ | D. | y=$\frac{cosx}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
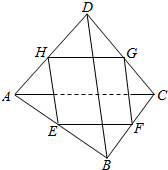 如图所示,在空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,判断平面EG与直线BD是否平行?平面EG与直线AC是否平行?直线BD与直线AC是什么位置关系?
如图所示,在空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,判断平面EG与直线BD是否平行?平面EG与直线AC是否平行?直线BD与直线AC是什么位置关系?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com