
分析 由已知可得0<$α-\frac{π}{6}$<$\frac{π}{3}$,利用同角三角函数基本关系式可求cos($α-\frac{π}{6}$),$tan(α-\frac{π}{6})$的值,利用诱导公式可求sin($\frac{π}{3}$+α),cos($\frac{π}{3}$+α)的值,利用二倍角的正弦函数公式即可化简求值.
解答 解:∵$\frac{π}{6}<α<\frac{π}{2}$,$sin(α-\frac{π}{6})=\frac{1}{3}$,
∴0<$α-\frac{π}{6}$<$\frac{π}{3}$,
∴cos($α-\frac{π}{6}$)=$\sqrt{1-si{n}^{2}(α-\frac{π}{6})}$=$\frac{2\sqrt{2}}{3}$,
∴$tan(α-\frac{π}{6})$=$\frac{sin(α-\frac{π}{6})}{cos(α-\frac{π}{6})}$=$\frac{\sqrt{2}}{4}$,
∵sin($\frac{π}{3}$+α)=cos[$\frac{π}{2}$-($\frac{π}{3}$+α)]=cos($\frac{π}{6}$-α)=$\frac{2\sqrt{2}}{3}$,
cos($\frac{π}{3}$+α)=sin[$\frac{π}{2}$-($\frac{π}{3}$+α)]=sin($\frac{π}{6}$-α)=-$\frac{1}{3}$,
∴$sin(\frac{2π}{3}+2α)$=2sin($\frac{π}{3}$+α)cos($\frac{π}{3}$+α)=2×$\frac{2\sqrt{2}}{3}$×(-$\frac{1}{3}$)=$-\frac{{4\sqrt{2}}}{9}$.
故答案为:$\frac{{\sqrt{2}}}{4}$,$-\frac{{4\sqrt{2}}}{9}$.
点评 本题主要考查了同角三角函数基本关系式,诱导公式,二倍角的正弦函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:解答题
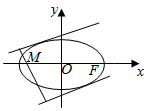 已知点F(1,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且椭圆C上的点到点F的最大距离为$\sqrt{2}+1$.
已知点F(1,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且椭圆C上的点到点F的最大距离为$\sqrt{2}+1$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
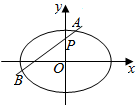 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为4.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任意两个一次函数最多存在一条“分界线” | |
| B. | “分界线”存在的两个函数的图象最多只有两个交点 | |
| C. | f(x)=x2-2x与g(x)=-x2+4的“分界线”是y=-x+2 | |
| D. | f(x)=x2与g(x)=-(x-1)2的“分界线”是y=0或$y=x-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
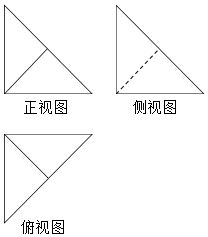 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com