
(13分)已知函数 .
.
(Ⅰ)若 求函数
求函数 的单调区间;
的单调区间;
(Ⅱ)若 在
在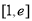 上的最小值为
上的最小值为 ,求
,求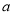 的值;
的值;
(Ⅲ)若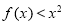 在
在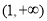 上恒成立,求
上恒成立,求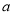 的取值范围.
的取值范围.
科目:高中数学 来源:2014-2015学年广东省江门市高三调研测试文科数学试卷(解析版) 题型:选择题
将正弦曲线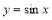 上所有的点横坐标伸长到原来的2倍,纵坐标不变,所得曲线对应的函数的最小正周期
上所有的点横坐标伸长到原来的2倍,纵坐标不变,所得曲线对应的函数的最小正周期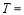
A.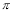 B.
B.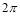 C.
C.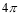 D.
D.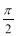
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省株洲市高三教学质量统一检测一文科数学试卷(解析版) 题型:选择题
下列函数中,与函数y=-3|x|的奇偶性相同,且在(-∞,0)上
单调性也相同的是( )
A.y=-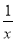 B.y=log2|x| C.y=1-x2 D.y=x3-1
B.y=log2|x| C.y=1-x2 D.y=x3-1
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高三上学期期中考试理科数学试卷(解析版) 题型:选择题
在如图所示的空间直角坐标系 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )
中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )

A.①和② B.③和① C. ④和③ D.④和②
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高三1月月考理科数学试卷(解析版) 题型:填空题
已知凸函数的性质定理:“若函数f(x)区间D上是凸函数,则对于区间D内的任意x1,x2,…,xn,有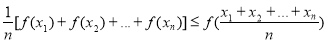 ”,若函数y=sinx 在区间(0,
”,若函数y=sinx 在区间(0,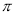 )上是凸函数,则在
)上是凸函数,则在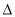 ABC中,sinA+sinB+sinC的最大值是 .
ABC中,sinA+sinB+sinC的最大值是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高三1月月考理科数学试卷(解析版) 题型:选择题
设函数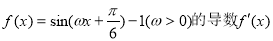 的最大值为3,则f(x)的图象的一条对称轴的方程是( ).
的最大值为3,则f(x)的图象的一条对称轴的方程是( ).
A.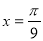 B.
B.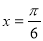 C.
C.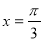 D.
D.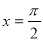
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com