
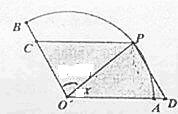
 半径为1,圆心角为120°的扇形,点P是扇形AB弧上的动点,设∠POA=x.
半径为1,圆心角为120°的扇形,点P是扇形AB弧上的动点,设∠POA=x.| PC |
| sin(120°-x) |
| 1 |
| sin60° |
| OC |
| sinx |
| 2 | ||
|
| 2 | ||
|
| 4 |
| 3 |
| 4 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |


科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
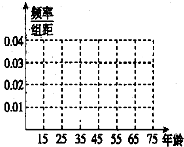 2014年我国公布了新的高考改革方案,在招生录取制度改革方面,普通高校逐步推行基于统一高考和高中学业水平考试成绩的综合评价、多元录取机制,普通高校招生录取将参考考生的高中学业水平考试成绩和职业倾向性测试成绩.为了解公众对“改革方案”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
2014年我国公布了新的高考改革方案,在招生录取制度改革方面,普通高校逐步推行基于统一高考和高中学业水平考试成绩的综合评价、多元录取机制,普通高校招生录取将参考考生的高中学业水平考试成绩和职业倾向性测试成绩.为了解公众对“改革方案”的态度,随机抽查了50人,将调查情况进行整理后制成下表:| 年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com