
分析 ①,利用单位圆及三角函数线,可得可得0<α<$\frac{π}{2}$时,则sinα<α<tanα,
②,若α是第二象限角,则$α∈(2kπ+\frac{π}{2},2kπ+π)$,$\frac{α}{2}$$∈(kπ+\frac{π}{4},kπ+\frac{π}{2}),k∈Z$,$\frac{α}{2}$是第一或第三象限角;
③,与向量$\overrightarrow{a}$=(3,4)共线的单位向量有$\overrightarrow{a}$=$(\frac{3}{5}$,$\frac{4}{5}$),$\overrightarrow{a}=(-\frac{3}{5},-\frac{4}{5})$;
④,函数f(x)=2x-8的零点3.
解答 解:对于①,如图,利用单位圆及三角函数线,可得AT>$\widehat{PA}$(劣弧)>PM,
可得若0<α<$\frac{π}{2}$,则sinα<α<tanα,故①正确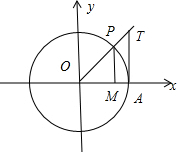
对于②,若α是第二象限角,则$α∈(2kπ+\frac{π}{2},2kπ+π)$,$\frac{α}{2}$$∈(kπ+\frac{π}{4},kπ+\frac{π}{2}),k∈Z$,
∴$\frac{α}{2}$是第一或第三象限角,故②正确;
对于③,与向量$\overrightarrow{a}$=(3,4)共线的单位向量有$\overrightarrow{a}$=$(\frac{3}{5}$,$\frac{4}{5}$),$\overrightarrow{a}=(-\frac{3}{5},-\frac{4}{5})$,故③错;
对于④,函数f(x)=2x-8的零点为3.故④错.
故答案为:①②
点评 本题考查了命题真假的判定,涉及到了三角函数的基础知识,属于中档题.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{16}+\frac{y^2}{7}$=1或$\frac{x^2}{7}+\frac{y^2}{16}=1$ | ||
| C. | $\frac{x^2}{16}+\frac{y^2}{25}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{25}=1$或$\frac{x^2}{25}+\frac{y^2}{16}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某单位用木料制作如图所示的框架,框架的下部是边长为x,y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积是8m2
如图,某单位用木料制作如图所示的框架,框架的下部是边长为x,y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积是8m2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com