Question

5．某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上．在小艇出发时，轮船位于港口O北偏西30°且与该港口相距20海里的A处，并以30海里/小时的航行速度沿正东方向匀速行驶．经过t小时与轮船相遇．假设小艇的最高航行速度只能达到30海里/小时，试设计航行方案（即确定航行方向与航行速度的大小），使得小艇能以最短时间与轮船相遇，并说明理由．

Answer 1

分析 根据题意，要用时最小，则首先速度最高，即为：30海里/小时，然后是距离最短，则OC²=AC²+OA²-2×AC×OAcos∠OAC即：（30t）²=400+900t²-1200tcos60°解得t，再解得相应角．

解答 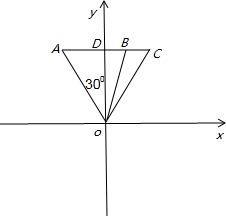解：（1）如图设小艇的速度为v，时间为t相遇，
则由余弦定理得：OC²=AC²+OA²-2×AC×OAcos∠OAC
即：（30t）²=400+900t²-1200tcos60°
∴600t=400
解得：t=$\frac{2}{3}$，此时∠BOD=30°
此时，在△OAB中，OA=OB=AB=20，故可设计航行方案如下：
航行方向为北偏东30°，航行速度为30海里/小时，小艇能以最短时间与轮船相遇．

点评 本题主要考查余弦定理，考查了数形结合的思想，考查学生分析解决问题的能力，比较基础．