
分析 (1)直接利用二次不等式化简求解即可.
(2)利用作差法化简,证明即可.
解答 解:(1)不等式:3≤x2-2x<8,
即:$\left\{\begin{array}{l}{{x}^{2}-2x-3≥0}\\{{x}^{2}-2x-8<0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x≤-1或x≥3}\\{-2<x<4}\end{array}\right.$,即x∈(-2,-1]∪[3,4).
(2)证明:∵(a2+b2)(c2+d2)-(ac+bd)2
=a2c2+a2d2+b2c2+b2d2-a2c2-2abcd-b2d2
=a2d2+b2c2-2abcd
=(ad-bc)2≥0
∴(a2+b2)(c2+d2)≥(ac+bd)2.
点评 本题考查二次不等式组的解法,作差法证明不等式的方法,考查转化思想以及计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=|x| | B. | y=-x3 | C. | y=($\frac{1}{2}$)x | D. | y=$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
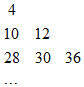 设数列{an}是集合{x|x=3s+3t,s<t且s,t∈N}中所有的数从小到大排列成的数列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,将数列{an}中各项按照上小下大,左小右大的原则排成如图的等腰直角三角形数表,则a15的值为324.
设数列{an}是集合{x|x=3s+3t,s<t且s,t∈N}中所有的数从小到大排列成的数列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,将数列{an}中各项按照上小下大,左小右大的原则排成如图的等腰直角三角形数表,则a15的值为324.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
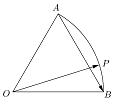 如图,已知半径为1的扇形AOB,∠AOB=60°,P为弧$\widehat{AB}$上的一个动点,则$\overrightarrow{OP}•\overrightarrow{AB}$取值范围是[$-\frac{1}{2}$,$\frac{1}{2}$].
如图,已知半径为1的扇形AOB,∠AOB=60°,P为弧$\widehat{AB}$上的一个动点,则$\overrightarrow{OP}•\overrightarrow{AB}$取值范围是[$-\frac{1}{2}$,$\frac{1}{2}$].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com