
分析 (1)由焦点求出c,结合椭圆离心率求得a,再由隐含条件求得b,则椭圆方程可求;
(2)由θ=90°,可得直线l垂直x轴,求出M,N的坐标,代入$\frac{1}{MF}+\frac{1}{NF}$=$\frac{{5\sqrt{2}}}{9}$,即可求得实数m的值;
(3)当θ=90°时,由(2)知$\frac{1}{NF}+\frac{1}{MF}=\frac{10}{9m}$;当θ≠90°时,设直线的斜率为k,M(x1,y1),N(x2,y2),则直线MN:y=k(x-4m),联立椭圆方程,得到关于x的一元二次方程,利用根与系数的关系求出M,N的横坐标的和与积,代入$\frac{1}{MF}+\frac{1}{NF}$,说明$\frac{1}{MF}+\frac{1}{NF}$的值与直线l的倾斜角θ的大小无关.
解答 解:(1)由c=4m,$e=\frac{4}{5}$,得:a=5m,∴b2=a2-c2=9m2,
∴椭圆方程为$\frac{x^2}{{25{m^2}}}+\frac{y^2}{{9{m^2}}}=1$;
(2)当x=4m时,${y^2}=\frac{{81{m^2}}}{25}$,得:$|y|=\frac{9m}{5}$,
于是当θ=90°时,$NF=MF=\frac{9m}{5}$,于是$\frac{1}{NF}+\frac{1}{MF}=\frac{9m}{5}=\frac{{9\sqrt{2}}}{5}$,
得到$m=\sqrt{2}$;
(3)①当θ=90°时,由(2)知$\frac{1}{NF}+\frac{1}{MF}=\frac{10}{9m}$;
②当θ≠90°时,设直线的斜率为k,M(x1,y1),N(x2,y2),则直线MN:y=k(x-4m),
联立椭圆方程有(9+25k2)x2-200k2mx+25m2(16k2-9)=0,
${x_1}+{x_2}=\frac{{200{k^2}m}}{{(9+25{k^2})}}$,${x_1}•{x_2}=\frac{{25{m^2}(16{k^2}-9)}}{{(9+25{k^2})}}$,
$\frac{1}{MF}+\frac{1}{NF}$=$\frac{1}{{5m-\frac{4}{5}{x_1}}}$+$\frac{1}{{5m-\frac{4}{5}{x_2}}}$=$\frac{10m-\frac{4}{5}({x}_{1}+{x}_{2})}{25{m}^{2}-4m({x}_{1}+{x}_{2})+\frac{16}{25}{x}_{1}{x}_{2}}$=$\frac{90m(1+{k}^{2})}{81{m}^{2}(1+{k}^{2})}$.
得$\frac{1}{NF}+\frac{1}{MF}=\frac{10}{9m}$.
综上,$\frac{1}{NF}+\frac{1}{MF}=\frac{10}{9m}$为定值,与直线l的倾斜角θ的大小无关.
点评 本题考查椭圆标准方程的求法,考查了直线与椭圆位置关系的应用,体现了“设而不求”的解题思想方法,是中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为棱DD1上一点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为棱DD1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
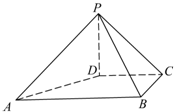 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com