
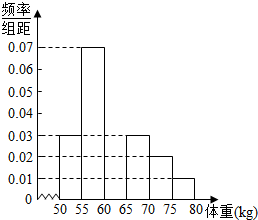
 某校对高二年段的男生进行体检,现将高二男生的体重(kg)数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[60,65)的人数为200.根据一般标准,高二男生体重超过65kg属于偏胖,低于55kg属于偏瘦.观察图形的信息,回答下列问题:
某校对高二年段的男生进行体检,现将高二男生的体重(kg)数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[60,65)的人数为200.根据一般标准,高二男生体重超过65kg属于偏胖,低于55kg属于偏瘦.观察图形的信息,回答下列问题:分析 (1)利用频率分布直方图的性质能求出求出体重在[60,65)内的频率,由此能补全的频率分布直方图.
(2)设男生总人数为n,由$\frac{200}{n}=0.2$,可得n=1000,从而体重超过65kg的总人数300,由此能求出各组应分别抽取的人数.
(3)利用频率分布直方图能估计高二男生的体重的中位数与平均数.
解答 解:(1)体重在[60,65)内的频率=1-(0.03+0.07+0.03+0.02+0.01)×5=0.2
$\frac{频率}{组距}$=$\frac{0.2}{5}=0.04$,
补全的频率分布直方图如图所示.…(4分)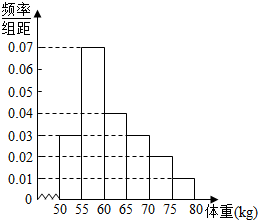
(2)设男生总人数为n,
由$\frac{200}{n}=0.2$,可得n=1000
体重超过65kg的总人数为(0.03+0.02+0.01)×5×1000=300
在[65,70)的人数为0.03×5×1000=150,应抽取的人数为$6×\frac{150}{300}=3$,
在[65,70)的人数为0.02×5×1000=100,应抽取的人数为$6×\frac{100}{300}=2$,
在[75,80)的人数为0.01×5×1000=50,应抽取的人数为$6×\frac{50}{300}=1$.
所以在[65,70),[70,75),[75,80]三段人数分别为3,2,1.…(8分)
(3)中位数为60kg
平均数为(52.5×0.03+57.5×0.07+62.5×0.04+67.5×0.03+72.5×0.02+77.5×0.01)×5=61.75(kg)…(12分)
点评 本题考查频率的求法,考查频率分布直方图的作法,考查中位数、平均数的求法,是基础题,解题时要认真审题,注意分层抽样、频率分布直方图的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
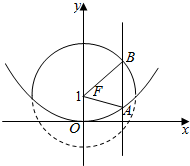 如图,直线x=m与抛物线x2=4y交于点A,与圆(y-1)2+x2=4的实线部分(即在抛物线开口内的圆弧)交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )
如图,直线x=m与抛物线x2=4y交于点A,与圆(y-1)2+x2=4的实线部分(即在抛物线开口内的圆弧)交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )| A. | (2,4) | B. | (4,6) | C. | [2,4] | D. | [4,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
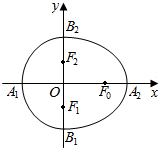 我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x>0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是腰长为1的等腰直角三角形,则a,b的值分别为( )
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x>0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是腰长为1的等腰直角三角形,则a,b的值分别为( )| A. | 5,4 | B. | $\frac{{\sqrt{7}}}{2},1$ | C. | $1,\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{6}}}{2},1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com