
分析 (1)利用抛物线的定义建立方程,求出p,即可求出抛物线C的方程;
(2)联立$\left\{\begin{array}{l}y=kx+2\\{y^2}=2x\end{array}\right.$得ky2-2y+4=0,利用OM⊥ON,$\overrightarrow{OM}•\overrightarrow{ON}=0$,即x1•x2+y1•y2=0,求出k,即可求直线的方程.
解答 解:(1)依据抛物线的定义知:A到抛物线焦点F的距离为$AF=\frac{1}{2}+\frac{p}{2}=1$,
所以p=1,抛物线的方程为y2=2x;---------(5分)
(2)依题意,直线l的方程设为y=kx+2(k≠0),M(x1,y1),N(x2,y2),
联立$\left\{\begin{array}{l}y=kx+2\\{y^2}=2x\end{array}\right.$得ky2-2y+4=0,
由△=4-16k>0,得$k<\frac{1}{4}$;${y_1}{y_2}=\frac{4}{k}$--------(7分)
∵OM⊥ON,∴$\overrightarrow{OM}•\overrightarrow{ON}=0$,即x1•x2+y1•y2=0---------(9分)
∴$\frac{{{{({{y_1}{y_2}})}^2}}}{4}+{y_1}{y_2}=0$,即$\frac{16}{{4{k^2}}}+\frac{4}{k}=0$,解得k=-1---------(11分)
所以直线l的方程为y=-x+2,即x+y-2=0---------1(2分)
点评 此题主要考查直线与抛物线相交后的一系列问题,其中涉及到韦达定理的考查,在交点问题的求法中应用很广泛,需要理解记忆.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
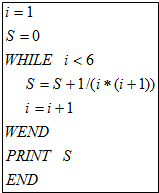
| A. | $\frac{53}{60}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
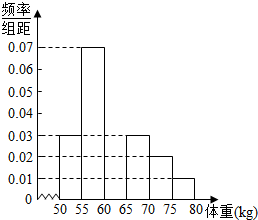 某校对高二年段的男生进行体检,现将高二男生的体重(kg)数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[60,65)的人数为200.根据一般标准,高二男生体重超过65kg属于偏胖,低于55kg属于偏瘦.观察图形的信息,回答下列问题:
某校对高二年段的男生进行体检,现将高二男生的体重(kg)数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[60,65)的人数为200.根据一般标准,高二男生体重超过65kg属于偏胖,低于55kg属于偏瘦.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -ln(e+1) | B. | -ln(4+e) | C. | -1 | D. | $-ln(e+\frac{1}{4})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com