
分析 (Ⅰ)设A(x1,y1),B(x2,y2),由 $\left\{\begin{array}{l}x=ny+2\\{y^2}=x\end{array}\right.$可得y2-ny-2=0,再由韦达定理得$\overrightarrow{OA}•\overrightarrow{OB}$的值;
(Ⅱ)三条直线AN,MN,BN的斜率成等差数列,证明k1+k3=2k2即可.
解答 解:(Ⅰ)设A(x1,y1)、B(x2,y2)
由 $\left\{\begin{array}{l}x=ny+2\\{y^2}=x\end{array}\right.$可得 y2-ny-2=0
由韦达定理可得 y1+y2=n,y1y2=-2…(3分)
∴$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=y12y22+y1y2=4-2=2,…(5分)
(Ⅱ)当n=0时,A(2,$\sqrt{2}$)、$B(2,-\sqrt{2})$
不妨取N(-2,2),则k1=$\frac{2-\sqrt{2}}{-4}$,k2=$\frac{2}{-4}$,k3=$\frac{2+\sqrt{2}}{-4}$
易得k1+k3=2k2. …(7分)
设N(-2,y0),k2=-$\frac{{y}_{0}}{4}$
k1+k3=$\frac{{y}_{1}-{y}_{0}}{{x}_{1}+2}$+$\frac{{y}_{2}-{y}_{0}}{{x}_{2}+2}$=$\frac{{2n{y_1}{y_2}+(4-n{y_0})({y_1}+{y_2})-8{y_0}}}{{{n^2}{y_1}{y_2}+4n({y_1}+{y_2})+16}}$=$\frac{-4n+(4-n{y}_{0})n-8{y}_{0}}{-2{n}^{2}+4{n}^{2}+16}$=-$\frac{{y}_{0}}{2}$=2k2
∴k1+k3=2k2,k1,k2,k3成等差数列. …(12分)
点评 本题考查直线和圆锥曲线的位置关系,考查向量知识的运用,考查韦达定理,考查学生分析解决问题的能力,属于中档题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
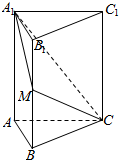 如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠ABC=90°,AB=4,AA1=6,点M时BB1中点.
如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠ABC=90°,AB=4,AA1=6,点M时BB1中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
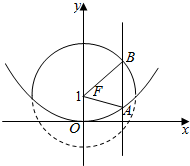 如图,直线x=m与抛物线x2=4y交于点A,与圆(y-1)2+x2=4的实线部分(即在抛物线开口内的圆弧)交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )
如图,直线x=m与抛物线x2=4y交于点A,与圆(y-1)2+x2=4的实线部分(即在抛物线开口内的圆弧)交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )| A. | (2,4) | B. | (4,6) | C. | [2,4] | D. | [4,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{7}$ | C. | 7 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com