
分析 (Ⅰ)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)由题意,得$\left\{\begin{array}{l}{\frac{{a}^{2}}{c}=4}\\{c=1}\end{array}\right.$,由此能求出椭圆方程;
(Ⅱ)由|$\overrightarrow{MQ}$|=2|$\overrightarrow{QF}$|,可得$\overrightarrow{MQ}$=2$\overrightarrow{QF}$,或$\overrightarrow{MQ}$=-2$\overrightarrow{QF}$,分别讨论,运用向量共线的坐标表示和椭圆方程,由此能求出直线l的斜率.
解答 解:(Ⅰ)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)
由题意,得$\left\{\begin{array}{l}{\frac{{a}^{2}}{c}=4}\\{c=1}\end{array}\right.$,解得a=2,c=1,b2=4-1=3,
∴椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(Ⅱ)∵|$\overrightarrow{MQ}$|=2|$\overrightarrow{QF}$|,
∴$\overrightarrow{MQ}$=2$\overrightarrow{QF}$,或$\overrightarrow{MQ}$=-2$\overrightarrow{QF}$,
当$\overrightarrow{MQ}$=2$\overrightarrow{QF}$时,点Q分$\overrightarrow{MF}$的比为2,
∴xQ=-$\frac{2}{3}$,yQ=$\frac{k}{3}$.
又点Q在椭圆上,
代入椭圆方程,得$\frac{(-\frac{2}{3})^{2}}{4}$+$\frac{(\frac{k}{3})^{2}}{3}$=1,
解得k=±2$\sqrt{6}$.
当$\overrightarrow{MQ}$=-2$\overrightarrow{QF}$时,xQ=-2,yQ=0,此时k=0.
∴直线l的斜率为±2$\sqrt{6}$或0.
点评 本题考查椭圆方程的求法,考查直线的斜率的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
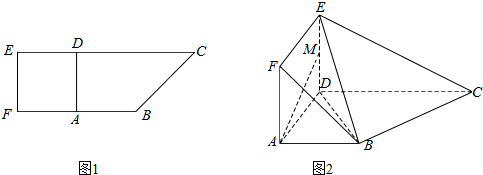
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
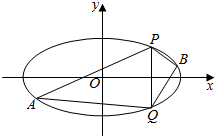 已知中心在原点,焦点在x轴上的椭圆C的离心率为$\frac{\sqrt{3}}{2}$,点(0,$\sqrt{2}$)是椭圆与y轴的一个交点.
已知中心在原点,焦点在x轴上的椭圆C的离心率为$\frac{\sqrt{3}}{2}$,点(0,$\sqrt{2}$)是椭圆与y轴的一个交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
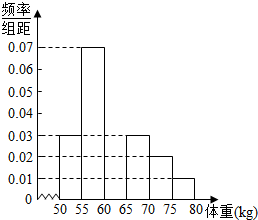 某校对高二年段的男生进行体检,现将高二男生的体重(kg)数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[60,65)的人数为200.根据一般标准,高二男生体重超过65kg属于偏胖,低于55kg属于偏瘦.观察图形的信息,回答下列问题:
某校对高二年段的男生进行体检,现将高二男生的体重(kg)数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[60,65)的人数为200.根据一般标准,高二男生体重超过65kg属于偏胖,低于55kg属于偏瘦.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 18 | C. | $\frac{27}{4}$ | D. | 12或$\frac{27}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com