
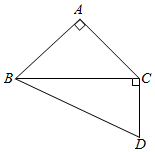
 如图,△ABC是等腰直角三角形,AB=AC,∠BCD=90°,且BC=$\sqrt{3}$CD=3.将△ABC沿BC的边翻折,设点A在平面BCD上的射影为点M,若点M在△BCD内部(含边界),则点M的轨迹的最大长度等于$\frac{\sqrt{3}}{2}$;在翻折过程中,当点M位于线段BD上时,直线AB和CD所成的角的余弦值等于$\frac{\sqrt{6}}{6}$.
如图,△ABC是等腰直角三角形,AB=AC,∠BCD=90°,且BC=$\sqrt{3}$CD=3.将△ABC沿BC的边翻折,设点A在平面BCD上的射影为点M,若点M在△BCD内部(含边界),则点M的轨迹的最大长度等于$\frac{\sqrt{3}}{2}$;在翻折过程中,当点M位于线段BD上时,直线AB和CD所成的角的余弦值等于$\frac{\sqrt{6}}{6}$. 分析 点A的射影M的轨迹为CD的中位线,可得其长度;当点M位于线段BD上时,取BC中点为N,AC中点为P,可得∠MNP或其补角即为直线AB和CD所成的角,由已知数据和余弦定理可得.
解答 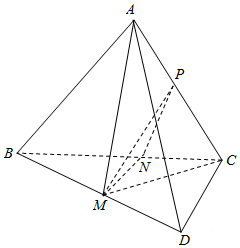 解:由题意可得点A的射影M的轨迹为CD的中位线,其长度为$\frac{1}{2}$CD=$\frac{\sqrt{3}}{2}$;
解:由题意可得点A的射影M的轨迹为CD的中位线,其长度为$\frac{1}{2}$CD=$\frac{\sqrt{3}}{2}$;
当点M位于线段BD上时,AM⊥平面ACD,取BC中点为N,AC中点为P,
∴∠MNP或其补角即为直线AB和CD所成的角,
则由中位线可得MN=$\frac{1}{2}$CD=$\frac{\sqrt{3}}{2}$,PC=$\frac{1}{2}$AB=$\frac{3\sqrt{2}}{4}$,
又MP为RT△AMC斜边AC的中线,故MP=$\frac{1}{2}$AC=$\frac{3\sqrt{2}}{4}$,
∴在△MNP中,由余弦定理可得cos∠MNP=$\frac{(\frac{\sqrt{3}}{2})^{2}+(\frac{3\sqrt{2}}{4})^{2}-(\frac{3\sqrt{2}}{4})^{2}}{2×\frac{\sqrt{3}}{2}×\frac{3\sqrt{2}}{4}}$=$\frac{\sqrt{6}}{6}$,
故答案为:$\frac{\sqrt{3}}{2}$;$\frac{\sqrt{6}}{6}$.
点评 本题考查异面直线及其所成的角,理清翻转前后的数值的关系是解决问题的关键,属中档题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 10 | C. | 160 | D. | 320 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\sqrt{2}$x | B. | y=±x | C. | y=±$\frac{\sqrt{2}}{2}$x | D. | y=±$\frac{1}{2}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com