
分析 求得已知双曲线的渐近线方程,设出所求双曲线的方程为$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a,b>0),求出渐近线方程和准线方程,由题意可得$\frac{a}{b}$=$\frac{2\sqrt{5}}{5}$,$\frac{{a}^{2}}{c}$=$\frac{4\sqrt{2}}{3}$,结合a,b,c的关系,解方程可得a,b,进而得到双曲线的方程.
解答 解:双曲线$\frac{x^2}{5}-\frac{y^2}{4}=1$的渐近线为y=±$\frac{2\sqrt{5}}{5}$x,
设所求双曲线的方程为$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a,b>0),
渐近线方程为y=±$\frac{a}{b}$x,准线方程为y=±$\frac{{a}^{2}}{c}$,
由题意可得$\frac{a}{b}$=$\frac{2\sqrt{5}}{5}$,$\frac{{a}^{2}}{c}$=$\frac{4\sqrt{2}}{3}$,
又a2+b2=c2,解得a=2$\sqrt{2}$,b=$\sqrt{10}$,
即有所求双曲线的方程为$\frac{{y}^{2}}{8}$-$\frac{{x}^{2}}{10}$=1.
故答案为:$\frac{{y}^{2}}{8}$-$\frac{{x}^{2}}{10}$=1.
点评 本题考查双曲线的方程的求法,注意运用待定系数法,考查双曲线的渐近线方程和准线方程的运用,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
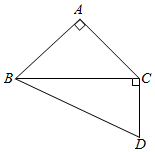 如图,△ABC是等腰直角三角形,AB=AC,∠BCD=90°,且BC=$\sqrt{3}$CD=3.将△ABC沿BC的边翻折,设点A在平面BCD上的射影为点M,若点M在△BCD内部(含边界),则点M的轨迹的最大长度等于$\frac{\sqrt{3}}{2}$;在翻折过程中,当点M位于线段BD上时,直线AB和CD所成的角的余弦值等于$\frac{\sqrt{6}}{6}$.
如图,△ABC是等腰直角三角形,AB=AC,∠BCD=90°,且BC=$\sqrt{3}$CD=3.将△ABC沿BC的边翻折,设点A在平面BCD上的射影为点M,若点M在△BCD内部(含边界),则点M的轨迹的最大长度等于$\frac{\sqrt{3}}{2}$;在翻折过程中,当点M位于线段BD上时,直线AB和CD所成的角的余弦值等于$\frac{\sqrt{6}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\sqrt{3}$x | B. | y=±$\sqrt{2}$x | C. | y=±$\frac{\sqrt{3}}{3}$x | D. | y=±$\frac{\sqrt{2}}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,+∞) | B. | (1,$\sqrt{2}$) | C. | [$\sqrt{3}$,+∞) | D. | (1,$\sqrt{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com