
 甲、乙两人在5次综合测评中成绩的茎叶图如图所示,其中一个数字被污染,记甲、乙的平均成绩为$\overrightarrow{{x}_{甲}}$,$\overrightarrow{{x}_{乙}}$,则$\overrightarrow{{x}_{甲}}$>$\overrightarrow{{x}_{乙}}$的概率是$\frac{2}{5}$.
甲、乙两人在5次综合测评中成绩的茎叶图如图所示,其中一个数字被污染,记甲、乙的平均成绩为$\overrightarrow{{x}_{甲}}$,$\overrightarrow{{x}_{乙}}$,则$\overrightarrow{{x}_{甲}}$>$\overrightarrow{{x}_{乙}}$的概率是$\frac{2}{5}$. 分析 由茎叶图求出$\overrightarrow{{x}_{甲}}$,$\overrightarrow{{x}_{乙}}$,由$\overrightarrow{{x}_{甲}}$>$\overrightarrow{{x}_{乙}}$,得90<89+$\frac{x}{5}$,x∈N,由此能过河卒子 同$\overrightarrow{{x}_{甲}}$>$\overrightarrow{{x}_{乙}}$的概率.
解答 解:由已知中的茎叶图可得
乙的5次综合测评中的成绩分别为87,86,92,94,91,
则乙的平均成绩:$\overrightarrow{{x}_{乙}}$=$\frac{1}{5}$(87+86+92+94+91)=90
设污损数字为x
则甲的5次综合测评中的成绩分别为85,87,84,99,90+X
甲的平均成绩:$\overrightarrow{{x}_{甲}}$=$\frac{1}{5}$(85+87+84+99+90+x)=89+$\frac{x}{5}$,
∵$\overrightarrow{{x}_{甲}}$>$\overrightarrow{{x}_{乙}}$,∴90<89+$\frac{x}{5}$,x∈N,
解得x的可能取值为6,7,8,9,
∴$\overrightarrow{{x}_{甲}}$>$\overrightarrow{{x}_{乙}}$的概率是p=$\frac{4}{10}$=$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意茎叶力的性质的合理运用.


科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(理)试卷(解析版) 题型:选择题
设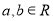 ,则“
,则“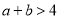 ”是“
”是“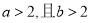 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既非充分又非必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | c<b<a | C. | c<a<b | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
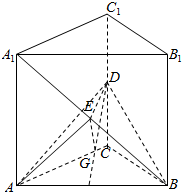 如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.
如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com