
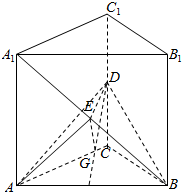
 如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.
如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.分析 (Ⅰ)连结BG,则BG是BE在ABD的射影,则∠EBG是A1B与平面ABD所成的角,由已知可得GE=DF,在直角三角形EFD中,通过求解直角三角形得$FD=\sqrt{3}$,进一步求得AB=$2\sqrt{2}$,${A}_{1}B=2\sqrt{3},EB=\sqrt{3}$,则A1B与平面ABD所成角的正弦值可求;
(Ⅱ)连结A1D,利用等积法求得A1到平面AED的距离.
解答 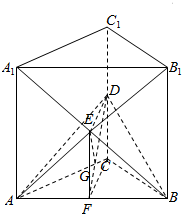 解:(Ⅰ)连结BG,则BG是BE在ABD的射影,
解:(Ⅰ)连结BG,则BG是BE在ABD的射影,
即∠EBG是A1B与平面ABD所成的角,
设F为AB的中点,连结EF、FC,
∵D,E分别是CC1与A1B的中点,
又DC⊥平面ABC,
∴CDEF为矩形,连接DE,G是ADB的重心,
∴GE=DF,
在直角三角形EFD中,$E{F}^{2}=FG•FD=\frac{1}{3}F{D}^{2}$,
∵EF=1,∴$FD=\sqrt{3}$,
于是$ED=\sqrt{2},EG=\frac{1×\sqrt{2}}{\sqrt{3}}=\frac{\sqrt{6}}{3}$,
∵$FC=CD=\sqrt{2}$,
∴AB=$2\sqrt{2}$,${A}_{1}B=2\sqrt{3},EB=\sqrt{3}$,
∴$sin∠EBG=\frac{EG}{EB}=\frac{\sqrt{6}}{3}•\frac{1}{\sqrt{3}}=\frac{\sqrt{2}}{3}$,
∴A1B与平面ABD所成角的正弦值为$\frac{\sqrt{2}}{3}$;
(Ⅱ)连结A1D,有${V}_{{A}_{1}-AED}={V}_{D-A{A}_{1}E}$,
∵ED⊥AB,ED⊥EF,
又EF∩AB=F,
∴ED⊥平面A1AB,
设A1到平面AED的距离为h,则${S}_{△AED}•h={S}_{△{A}_{1}AD}•ED$,
又${S}_{△{A}_{1}AE}=\frac{1}{2}{S}_{△{A}_{1}AB}=\frac{1}{4}{A}_{1}A•AB=\sqrt{2}$.
${S}_{△AED}=\frac{1}{2}AE•ED=\frac{\sqrt{6}}{2}$,
∴$h=\frac{\sqrt{2}×\sqrt{2}}{\frac{\sqrt{6}}{2}}=\frac{2\sqrt{6}}{3}$,即A1到平面AED的距离$\frac{2\sqrt{6}}{3}$.
点评 本题考查直线与平面所成的角,考查了点到平面距离的求法,考查空间想象能力和思维能力,考查计算能力,是中档题.


科目:高中数学 来源: 题型:填空题
 甲、乙两人在5次综合测评中成绩的茎叶图如图所示,其中一个数字被污染,记甲、乙的平均成绩为$\overrightarrow{{x}_{甲}}$,$\overrightarrow{{x}_{乙}}$,则$\overrightarrow{{x}_{甲}}$>$\overrightarrow{{x}_{乙}}$的概率是$\frac{2}{5}$.
甲、乙两人在5次综合测评中成绩的茎叶图如图所示,其中一个数字被污染,记甲、乙的平均成绩为$\overrightarrow{{x}_{甲}}$,$\overrightarrow{{x}_{乙}}$,则$\overrightarrow{{x}_{甲}}$>$\overrightarrow{{x}_{乙}}$的概率是$\frac{2}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份x年 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 平均成绩y分 | 97 | 98 | 103 | 108 | 109 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com