[题目]设直线与直线分别与椭圆交于点.且四边形的面积为.(1)求椭圆的方程,(2)过椭圆上一点作椭圆的切线.设直线与椭圆相较于.两点.为坐标原点.求的取值范围. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】设直线与直线分别与椭圆交于点，且四边形的面积为.

（1）求椭圆的方程；

（2）过椭圆上一点作椭圆的切线，设直线与椭圆相较于，两点，为坐标原点，求的取值范围.

【答案】（1）（2）

【解析】

联立直线AB与椭圆的方程，解出x与y，由椭圆的对称性可知四边形ACBD为矩形，进而表示出矩形ACBD的面积为，从而得解；

分类讨论，当直线l的斜率不存在，此时点P为椭圆的左或右顶点，易求得和，所以；

当直线l的斜率存在，设其方程为，点P的坐标为，M、N的坐标分别为，，两次联立直线与椭圆，分别可得到关于x的一元二次方程，结合直线l与椭圆相切，可得及，结合弦长公式，可得，然后作比，即可求得取值范围．

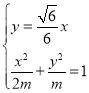由，解得，，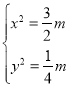

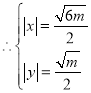由椭圆的对称性可知，四边形ACBD为矩形，且其面积，，

故椭圆的方程为．

当直线l的斜率不存在时，点P为椭圆的左或右顶点，其坐标为，

不妨取左顶点，即，此时，且直线l与x轴垂直，将代入得，，，

所以；

当直线l的斜率存在时，设其方程为，点P的坐标为，M、N的坐标分别为，，

联立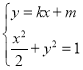，得，

直线l与椭圆相切，，

化简整理得，，

由韦达定理知，，

，

联立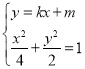，得，

由韦达定理知，，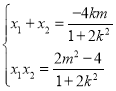

，

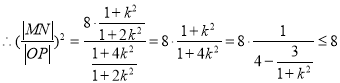，当且仅当时，等号成立，

综上所述，的取值范围为．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系中，已知圆的方程为，圆的方程为，动圆与圆内切且与圆外切.

(1)求动圆圆心的轨迹的方程；

(2)已知与为平面内的两个定点，过点的直线与轨迹交于,两点，求四边形面积的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆的左、右焦点分别为，且椭圆的离心率为，过作轴的垂线与椭圆交于两点，且，动点在椭圆上．

（1）求椭圆的标准方程；

（2）记椭圆的左、右顶点分别为，且直线的斜率分别与直线（为坐标原点）的斜率相同，动点不与重合，求的面积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】中国铁路总公司相关负责人表示，到2018年底，全国铁路营业里程达到13.1万公里，其中高铁营业里程2.9万公里，超过世界高铁总里程的三分之二，下图是2014年到2018年铁路和高铁运营里程（单位：万公里）的折线图，以下结论不正确的是（）

A.每相邻两年相比较，2014年到2015年铁路运营里程增加最显著

B.从2014年到2018年这5年，高铁运营里程与年价正相关

C.2018年高铁运营里程比2014年高铁运营里程增长80%以上

D.从2014年到2018年这5年，高铁运营里程数依次成等差数列

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆：的左顶点为，右焦点为，斜率为1的直线与椭圆交于，两点，且，其中为坐标原点.

（1）求椭圆的标准方程；

（2）设过点且与直线平行的直线与椭圆交于，两点，若点满足，且与椭圆的另一个交点为，求的值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】随着移动支付的普及，中国人的生活方式正在悄然发生改变，带智能手机而不带钱包出门渐渐成为中国人的新习惯．在调查“现金支付，银联卡支付，手机支付”三种支付方式中“最常用的支付方式”这个问题时，在中国某地，从20岁到40岁人群中随机抽取55人，从40岁到60岁人群随机抽取45人，进行答题．20岁到40岁人群的支付情况是选择现金支付的占、银联卡支付的占、手机支付的占．40岁到60岁人群的支付情况是：现金支付的占、银联卡支付的占、手机支付的占．