
| A. | ①③ | B. | ②③ | C. | ①⑤ | D. | ②③④ |
分析 根据G是关于运算⊕为“融洽集”的定义,逐一分析五个集合及运算是否满足定义,可得答案.
解答 解:①G={非负整数},⊕为整数的加法;满足(1),且存在e=0,满足(2),故G是关于运算⊕为“融洽集”;
②G={偶数},⊕为整数的乘法;若存在e满足(2),则e=1,矛盾,故G不是关于运算⊕为“融洽集”;
③G={平面向量},⊕为平面向量的加法;满足(1),且存在e=$\overrightarrow{0}$,满足(2),故G是关于运算⊕为“融洽集”;
④G={二次三项式},⊕为多项式的加法;两个二次三项式的和可能不是三项式,不满足(1),故G不是关于运算⊕为“融洽集”;
⑤G={虚数},⊕为复数的乘法.两个虚数的积可能为一个实数,不满足(1),故G不是关于运算⊕为“融洽集”;
这样G是关于运算⊕为“融洽集”的有①③.
故选:A
点评 本题以命题的真假判断与应用为载体,考查了G是关于运算⊕为“融洽集”的定义,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 3 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
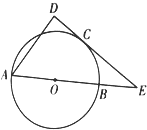 如图,AB为圆O的直径,E为AB的延长线上一点,过E作圆O的切线,切点为C,过A作直线EC的垂线,垂足为D.若AB=4,CE=2$\sqrt{3}$,求 AD.
如图,AB为圆O的直径,E为AB的延长线上一点,过E作圆O的切线,切点为C,过A作直线EC的垂线,垂足为D.若AB=4,CE=2$\sqrt{3}$,求 AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com