
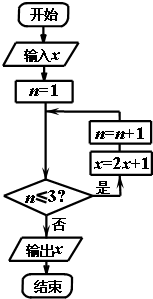
分析 根据框图的流程,依次计算运行的结果,直到不满足条件n≤3,求出输出x的值,再根据输出的x大于39,求出输入x的范围,根据几何概型的概率公式计算.
解答 解:由程序框图知:第一次运行x=2x-1,n=2;
第二次运行x=2×(2x-1)-1.n=2+1=3;
第三次运行x=2×[2×(2x-1)-1]-1,n=3+1=4,
不满足条件n≤3,程序运行终止,输出x=8x-(4+2+1)=8x-7,
由输出的x大于39,得x>5.75,
∴输入x∈[6,19],数集的长度为14,
又数集[1,19]的长度为18,
∴输出的x大于39的概率为$\frac{14}{18}$=$\frac{7}{9}$.
故答案为:$\frac{7}{9}$.
点评 本题考查了循环结构的程序框图,根据框图的流程判断算法的功能是解答此类问题的关键,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
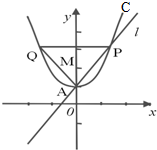 已知二次函数y=ax2+1的图象为抛物线C,过顶点A(0,1)的直线l与抛物线C相交于另外一点P,点Q为抛物线C上另外一点,且点M(0,m)到直线l的距离为1.
已知二次函数y=ax2+1的图象为抛物线C,过顶点A(0,1)的直线l与抛物线C相交于另外一点P,点Q为抛物线C上另外一点,且点M(0,m)到直线l的距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
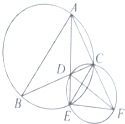 如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$.
如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,3) | B. | [-1,3] | C. | ∅ | D. | (2,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com