
| A. | [0,2] | B. | [0,1] | C. | [1,2] | D. | [-1,0] |
分析 由“亲密函数”的概念知,?x∈[a,b]都有|f(x)-g(x)|=|x2+x+1|≤1成立,可求得f(x),g(x)的“亲密区间”是[-1,0],从而得到答案.
解答 解:若f(x)=x2+3x+2,g(x)=2x+1在[a,b]上是“亲密函数”,
则|f(x)-g(x)|=|x2+3x+2-(2x+1)|=|x2+x+1|≤1.
因为x2+x+1=(x+$\frac{1}{2}$)2+$\frac{3}{4}$>0,
所以,|x2+x+1|≤1?x2+x+1≤1,即x2+x≤0,
解得:-1≤x≤0.
即?x∈[-1,0]都有|f(x)-g(x)|≤1成立,f(x),g(x)的“亲密区间”是[-1,0].
故选:D.
点评 本题考查函数恒成立问题,理解新定义“亲密函数”与“亲密区间”是关键,考查推理与运算能力,属于中档题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:选择题
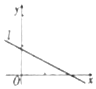 设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),则下列结论正确的是( )
设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),则下列结论正确的是( )| A. | x和y成正相关 | |
| B. | 若直线l方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,则$\widehat{b}$>0 | |
| C. | 最小二乘法是使尽量多的样本点落在直线上的方法 | |
| D. | 直线l过点$(\overline x,\overline y)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {-2,-1,0,1,2} | C. | {1,2} | D. | {-2,-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )| A. | 4π | B. | 2π | C. | $\frac{4π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
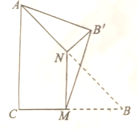 如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )
如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )| A. | $\frac{\sqrt{2}}{5}$ | B. | $\frac{\sqrt{3}}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com