Question

6．已知f（x）=|xe^x|，又g（x）=f²（x）-tf（x）（t∈R），若满足g（x）=-1的x有四个，则t的取值范围是（　　）

• A． $（-∞，-\frac{{{e^2}+1}}{e}）$
• B． $（\frac{{{e^2}+1}}{e}，+∞）$
• C． $（-\frac{{{e^2}+1}}{e}，-2）$
• D． $（2，\frac{{{e^2}+1}}{e}）$

Answer 1

分析 令y=xe^x，则y'=（1+x）e^x，求出极值点，判断函数的单调性，作出y=xe^x图象，利用图象变换得f（x）=|xe^x|图象，令f（x）=m，则关于m方程h（m）=m²-tm+1=0两根分别在$（0，\frac{1}{e}），（\frac{1}{e}，+∞）$，满足g（x）=-1的x有4个，列出不等式求解即可．

解答 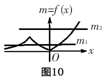解：令y=xe^x，则y'=（1+x）e^x，由y'=0，得x=-1，
当x∈（-∞，-1）时，y'＜0，函数y单调递减，
当x∈（-1，+∞）时，y'＞0，函
数y单调递增．作出y=xe^x图象，
利用图象变换得f（x）=|xe^x|图象（如图10），
令f（x）=m，则关于m方程h（m）=m²-tm+1=0
两根分别在$（0，\frac{1}{e}），（\frac{1}{e}，+∞）$时（如图11），
满足g（x）=-1的x有4个，由$h（\frac{1}{e}）=\frac{1}{e^2}-\frac{1}{e}t+1＜0$，
解得$t＞\frac{{{e^2}+1}}{e}$．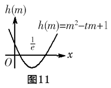  
故选：B．

点评 本题考查函数的导数的应用，函数的单调性以及函数的极值，函数的图象的变换，函数零点个数，考查函数与方程的综合应用，数形结合思想以及转化思想的应用．