
 ,对给定的正整数
,对给定的正整数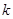 ,若在其定义域内存在实数
,若在其定义域内存在实数 ,使得
,使得 ,则称函数
,则称函数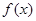 为“
为“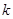 性质函数”。
性质函数”。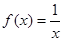 是否为“
是否为“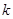 性质函数”?说明理由;
性质函数”?说明理由;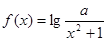 为“2性质函数”,求实数
为“2性质函数”,求实数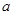 的取值范围;
的取值范围;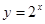 与
与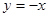 的图像有公共点,求证:
的图像有公共点,求证: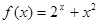 为“1性质函数”。
为“1性质函数”。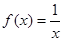 不能为“k性质函数”
不能为“k性质函数”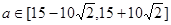
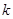 性质函数”的概念,列出方程,利用判别式法判断即可;(2)根据“2性质函数”的概念,列出方程,利用判别式列出关于a的不等式,再利用不等式知识求解即可;(3)由已知条件构造方程,最后化为满足“1性质函数”的方程即可证明函数成立
性质函数”的概念,列出方程,利用判别式法判断即可;(2)根据“2性质函数”的概念,列出方程,利用判别式列出关于a的不等式,再利用不等式知识求解即可;(3)由已知条件构造方程,最后化为满足“1性质函数”的方程即可证明函数成立 满足条件,则
满足条件,则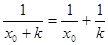 即
即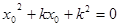 ,…………………. 2分
,…………………. 2分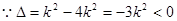 ,
,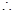 方程无实数根,与假设矛盾。
方程无实数根,与假设矛盾。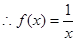 不能为
不能为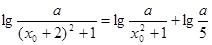 ,…………………. 5分
,…………………. 5分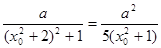 (
(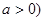 ,化简得
,化简得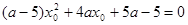 ,……………………………. 7分
,……………………………. 7分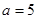 时,
时,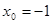 ;……………………………. 8分
;……………………………. 8分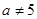 时,由
时,由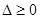 ,
,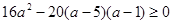 即
即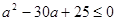 ,
,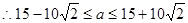 。
。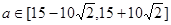 。……………………………. 10分
。……………………………. 10分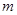 使
使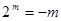 ,即
,即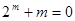 。…………………….11分
。…………………….11分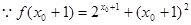 ,
,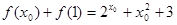 ,
,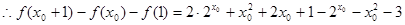
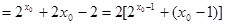 ,……………………………. 14分
,……………………………. 14分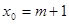 ,
,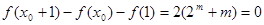 ,………………………. 15分
,………………………. 15分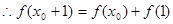 ,
,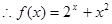 为“1性质函数”。………. 16分
为“1性质函数”。………. 16分

 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源:不详 题型:解答题
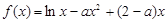 .
.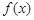 的单调性;
的单调性;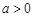 ,证明:当
,证明:当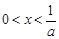 时,
时,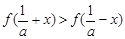 ;
;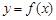 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,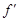 (x0)<0.
(x0)<0.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
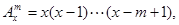 其中x∈R,m为正整数,且
其中x∈R,m为正整数,且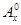 =1,这是排列数A
=1,这是排列数A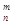 (n,m是正整数,且m≤n)的一种推广.
(n,m是正整数,且m≤n)的一种推广.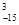 的值; (2)确定函数
的值; (2)确定函数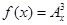 的单调区间.
的单调区间.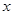 的方程
的方程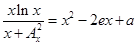 只有一个实数根, 求
只有一个实数根, 求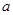 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com