
分析 双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左右焦点分别关于两条渐近线的对称点重合,可得一条渐近线的斜率为1,即b=a,即可求出双曲线的离心率.
解答 解:∵双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左右焦点分别关于两条渐近线的对称点重合,
∴一条渐近线的斜率为1,即b=a,
∴c=$\sqrt{2}$a,∴e=$\frac{c}{a}$=$\sqrt{2}$,
故答案为$\sqrt{2}$.
点评 本题考查双曲线的离心率,考查学生的计算能力,确定一条渐近线的斜率为1是关键.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
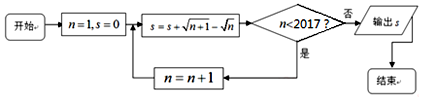
| A. | $\sqrt{2018}-1$ | B. | $\sqrt{2017}-1$ | C. | $\sqrt{2016}-1$ | D. | $\sqrt{2015}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | xy≠10是x≠5或y≠2的充分不必要条件 | |
| B. | 若命题p:?x∈R,x2+x+1≠0,则¬p:?x∈R,x2+x+1=0 | |
| C. | 已知随机变量X~N(2,σ2),且P(X≤4)=0.84,则P(X≤0)=0.16 | |
| D. | 相关指数R2越接近1,表示残差平方和越大. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2i | B. | -2 | C. | i | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 甲产品所需工时 | 乙产品所需工时 | |
| A设备 | 2 | 3 |
| B设备 | 4 | 1 |
| A. | 40万元 | B. | 45万元 | C. | 50万元 | D. | 55万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com