
袋中装着分别标有数字1,2,3,4,5的5个形状相同的小球.
(1)从袋中任取2个小球,求两个小球所标数字之和为3的倍数的概率;
(2)从袋中有放回的取出2个小球,记第一次取出的小球所标数字为x,第二次为y,求点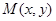 满足
满足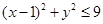 的概率.
的概率.
(1) 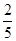 ; (2)
; (2) 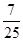 .
.
解析试题分析:(1)任取2次,基本事件有:[1,2] [1,3] [1,4] [1,5] [2,3] [2,4] [2,5] [3,4] [3,5] [4,5],记“两数之和为3的倍数”为事件A,则事件A中含有:[1,2] [1,5] [2,4] [4,5]共4个基本事件,所以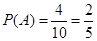 ;
;
(2) 有放回的取出2个,基本事件有:
(1,1) (1,2) (1,3) (1,4) (1,5)
(2,1) (2,2) (2,3) (2,4) (2,5)
(3,1) (3,2) (3,3) (3,4) (3,5)
(4,1) (4,2) (4,3) (4,4) (4,5)
(5,1) (5,2) (5,3) (5,4) (5,5)
记“点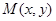 满足
满足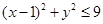 ”为事件
”为事件 ,则
,则 包含:(1,1) (1,2) (1,3)(2,1) (2,2) (3,1) (3,2)共7个基本事件 ,所以
包含:(1,1) (1,2) (1,3)(2,1) (2,2) (3,1) (3,2)共7个基本事件 ,所以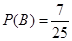 .
.
考点:本题考查了古典概型的求法
点评:对于古典概型的概率的计算,首先要分清基本事件总数及事件A包含的基本事件数,分清的方法常用列表法、画图法、列举法、列式计算等方法


科目:高中数学 来源: 题型:解答题
某大学高等数学老师这学期分别用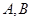 两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
(Ⅰ)依茎叶图判断哪个班的平均分高?
(Ⅱ)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率;
(Ⅲ)学校规定:成绩不低于85分的为优秀,请填写下面的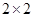 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
| | 甲班 | 乙班 | 合计 |
| 优秀 | | | |
| 不优秀 | | | |
| 合计 | | | |
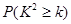 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
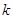 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
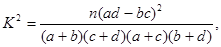 其中
其中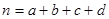 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
中央电视台星光大道某期节目中,有5位实力均等的选手参加比赛,经过四轮比赛决出周冠军(每一轮比赛淘汰l位选手).
(1)求甲、乙两位选手都进入第三轮比赛的概率;
(2)求甲选手在第三轮被淘汰的的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙、丙三人独立参加某企业的招聘考试,根据三人的专业知识、应试表现、工作经验等综合因素,三人被招聘的概率依次为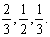 用
用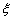 表示被招聘的人数。
表示被招聘的人数。
(1)求三人中至少有一人被招聘的概率;
(2)求随机变量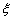 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
不透明的袋中有8张大小和形状完全相同的卡片,卡片上分别写有1,1,2,2,3,3,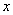 ,
,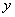 .现 从中任取3张卡片,假设每张卡片被取出的可能性相同.
.现 从中任取3张卡片,假设每张卡片被取出的可能性相同.
(I)求取出的三张卡片中至少有一张字母卡片的概率;
(Ⅱ)设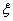 表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时
表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时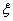 为这二个数字之和,否则
为这二个数字之和,否则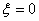 ,求
,求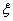 的分布列和期望
的分布列和期望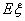 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
哈尔滨市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的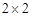 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为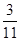 。
。
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
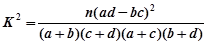 。
。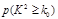 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
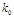 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人在罚球线互不影响地投球,命中的概率分别为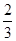 与
与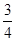 ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.
(1)甲、乙两人在罚球线各投球一次,求两人得分之和 的数学期望;
的数学期望;
(2)甲、乙两人在罚球线各投球二次,求甲恰好比乙多得分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为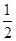 和
和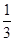 , 求:
, 求:
(1)甲、乙两人至少有一个人破译出密码的概率;
(2)两人都没有破译出密码的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com