
【题目】如图,正四棱锥![]() 的底边长为2,侧棱长为
的底边长为2,侧棱长为![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上的点,且
上的点,且![]() .
.
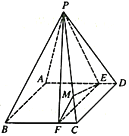
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求锐二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】某工厂拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为![]() 米,高为
米,高为![]() 米,体积为
米,体积为![]() 立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为![]() 元(
元(![]() 为圆周率).该蓄水池的体积最大时
为圆周率).该蓄水池的体积最大时![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,E,F分别为AB的三等分点,
中,E,F分别为AB的三等分点,![]() ,
,![]() ,
,![]() ,
,![]() 若沿着FG,ED折叠使得点A,B重合,如图2所示,连结GC,BD
若沿着FG,ED折叠使得点A,B重合,如图2所示,连结GC,BD
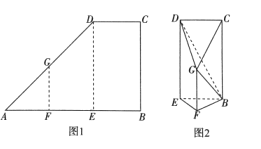
(1)求证:平面![]() 平面BCDE;
平面BCDE;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,判断函数
时,判断函数![]() ,(
,(![]() )有几个零点,并证明你的结论;
)有几个零点,并证明你的结论;
(3)设函数![]() ,若函数
,若函数![]() 在
在![]() 为增函数,求实数
为增函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数,满分100分,按照大于或等于80分的为优秀,小于80分的为合格,为了解学生的在该维度的测评结果,在毕业班中随机抽出一个班的数据.该班共有60名学生,得到如下的列联表:
优秀 | 合格 | 总计 | |
男生 | 6 | ||
女生 | 18 | ||
合计 | 60 |
已知在该班随机抽取1人测评结果为优秀的概率为![]() .
.
(1)完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
(3)现在如果想了解全校学生在该维度的表现情况,采取简单随机抽样方式在全校学生中抽取少数一部分来分析,请你选择一个合适的抽样方法,并解释理由.
附: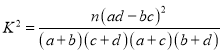
| 0.25 | 0.10 | 0.025 |
| 1.323 | 2.706 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“二进制”来源于我国古代的《易经》,该书中有两类最基本的符号:“—”和“——”,其中“—”在二进制中记作“1”,“——”在二进制中记作“0”,例如二进制数![]() 化为十进制的计算如下:
化为十进制的计算如下:![]() .若从两类符号中任取2个符号进行排列,则得到的二进制数所对应的十进制数大于2的概率为( )
.若从两类符号中任取2个符号进行排列,则得到的二进制数所对应的十进制数大于2的概率为( )
A.0B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省从2021年开始将全面推行新高考制度,新高考“![]() ”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为
”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为![]() 五个等级,确定各等级人数所占比例分别为
五个等级,确定各等级人数所占比例分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,等级考试科目成绩计入考生总成绩时,将
,等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法分别转换到
等级内的考生原始成绩,依照等比例转换法分别转换到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
等级 |
|
|
|
|
|
比例 |
|
|
|
|
|
赋分区间 |
|
|
|
|
|
而等比例转换法是通过公式计算:![]()
其中![]() ,
,![]() 分别表示原始分区间的最低分和最高分,
分别表示原始分区间的最低分和最高分,![]() 、
、![]() 分别表示等级分区间的最低分和最高分,
分别表示等级分区间的最低分和最高分,![]() 表示原始分,
表示原始分,![]() 表示转换分,当原始分为
表示转换分,当原始分为![]() ,
,![]() 时,等级分分别为
时,等级分分别为![]() 、
、![]()
假设小南的化学考试成绩信息如下表:
考生科目 | 考试成绩 | 成绩等级 | 原始分区间 | 等级分区间 |
化学 | 75分 |
|
|
|
设小南转换后的等级成绩为![]() ,根据公式得:
,根据公式得:![]() ,
,
所以![]() (四舍五入取整),小南最终化学成绩为77分.
(四舍五入取整),小南最终化学成绩为77分.
已知某年级学生有100人选了化学,以半期考试成绩为原始成绩转换本年级的化学等级成绩,其中化学成绩获得![]() 等级的学生原始成绩统计如下表:
等级的学生原始成绩统计如下表:
成绩 | 95 | 93 | 91 | 90 | 88 | 87 | 85 |
人数 | 1 | 2 | 3 | 2 | 3 | 2 | 2 |
(1)从化学成绩获得![]() 等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
(2)从化学成绩获得![]() 等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为
等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一年之计在于春,一日之计在于晨,春天是播种的季节,是希望的开端.某种植户对一块地的![]() 个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为
个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为![]() ,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
(1)当![]() 取何值时,有3个坑要补播种的概率最大?最大概率为多少?
取何值时,有3个坑要补播种的概率最大?最大概率为多少?
(2)当![]() 时,用
时,用![]() 表示要补播种的坑的个数,求
表示要补播种的坑的个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com