【答案】
分析:①将a
2-b
2=1,分解变形为(a+1)(a-1)=b
2,即可证明a-1<b,即a-b<1;
②先利用基本不等式求得2b(a-b)范围,进而代入原式,进一步利用基本不等式求得问题答案.
③求数列的最大值,可通过做差或做商比较法判断数列的单调性处理.
④题中原方程f
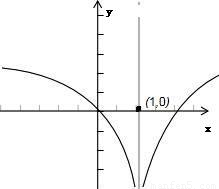
2(x)+2f(x)=0有多少个不同实数解,即要求对应于f(x)=0和f(x)=-2有几个不同实数解,故先根据题意作出f(x)的简图:由图可知,当f(x)=0时,它有三个根,当f(x)=-2时,它有二个根.故关于x的方程f
2(x)+2f(x)=0有且只有5个不同实数解.
⑤由题意得siny=

-sinx,且-1≤

-sinx≤1,得到sinx的取值范围,把所求的式子配方利用二次函数的性质求出其最大值.
解答:解:①若a
2-b
2=1,则a
2-1=b
2,即(a+1)(a-1)=b
2,
∵a+1>a-1,∴a-1<b,即a-b<1,①正确;
②:∵2b(a-2b)≤(
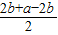
)
2=
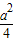
,
∴a
2+
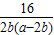
≥a
2+
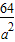
≥16.
当且仅当2b=a-2b时取等号.②正确;
③:a
n=n(n+4)(

)
n
则
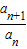
=
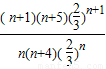
=

×
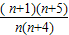
≥1
则2(n+1)(n+5)≥3n(n+4),即n
2≤10,所以n<4,
即n<4时,a
n+1>a
n,
当n≥4时,a
n+1<a
n,
所以a
4最大.③正确;
④:∵题中原方程f
2(x)+2f(x)=0有几个不同实数解,
∴即要求对应于f(x)=0和f(x)=-2有几个不同实数解,
故先根据题意作出f(x)的简图,如图,
由图可知,当f(x)=0时,它有三个根,当f(x)=-2时,它有二个根.关于x的方程f
2(x)+2f(x)=0有5个解.④不正确;
⑤:∵sinx+siny=

,∴siny=

-sinx,
∵-1≤

-sinx≤1,∴-

≤sinx≤1,
∴siny-cos
2x=

-sinx-(1-sin
2x)
=(sinx-

)2-
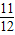
,∴sinx=-

时,siny-cos
2x的最大值为(-

-

)2-
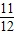
=

,⑤不正确.
故答案为:①②③.
点评:本题主要考查了命题的真假判断与应用,考查了基本不等式在最值问题中的应用、同角三角函数的基本关系,正弦函数的有界性,二次函数的性质等等.

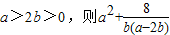 的最小值为16;
的最小值为16; ;
; ,则关于x的方程f2(x)+2f(x)=0有4个解.
,则关于x的方程f2(x)+2f(x)=0有4个解.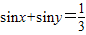 ,则siny-cos2x的最大值是
,则siny-cos2x的最大值是 .
. -sinx,且-1≤
-sinx,且-1≤ -sinx≤1,得到sinx的取值范围,把所求的式子配方利用二次函数的性质求出其最大值.
-sinx≤1,得到sinx的取值范围,把所求的式子配方利用二次函数的性质求出其最大值.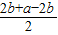 )2=
)2=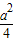 ,
,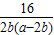 ≥a2+
≥a2+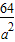 ≥16.
≥16.
 )n
)n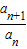 =
=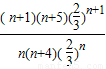 =
= ×
×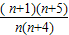 ≥1
≥1 ,∴siny=
,∴siny= -sinx,
-sinx, -sinx≤1,∴-
-sinx≤1,∴- ≤sinx≤1,
≤sinx≤1, -sinx-(1-sin2x)
-sinx-(1-sin2x)  )2-
)2-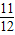 ,∴sinx=-
,∴sinx=- 时,siny-cos2x的最大值为(-
时,siny-cos2x的最大值为(- -
- )2-
)2-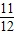 =
= ,⑤不正确.
,⑤不正确.
