
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 根据独立性检验的方法步骤,可判断①的正误.
根据方差的意义,可判断②的正误;
运用均值不等式,化简a+b=(a+b)($\frac{2}{a}$+$\frac{1}{b}$)进行计算即可判断③的正误.
根据正态分布的对称性,求出P(-1<ξ<0),可判断④的正误;
解答 解:①对分类变量x与y的随机变量k2的观测值k来说,k越大,判断“x与y有关系”的把握越大,故③错误.
②若将一组样本数据中的每个数据都加上同一个常数后,
数据的离散程度不变,则样本的方差不变,故②正确;
③a>0,b>0且$\frac{2}{a}$+$\frac{1}{b}$=1,则a+b=(a+b)($\frac{2}{a}$+$\frac{1}{b}$)=2+1+$\frac{2b}{a}$+$\frac{a}{b}$≥3+2$\sqrt{2}$,所以③不正确.
④设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(ξ<-1)=p,则P(-1<ξ<1)=1-2p,则P(-1<ξ<0)=$\frac{1}{2}$-p,故④正确;
故正确的命题的个数为2个,
故选:C.
点评 本题考查的知识点是命题的真假判断与应用,此类题型往往综合较多的其它知识点,综合性强,难度中档.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
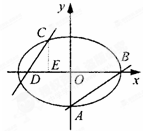 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$(a>b>0)的离心率$e=\frac{{\sqrt{6}}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{{\sqrt{3}}}{2}$.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$(a>b>0)的离心率$e=\frac{{\sqrt{6}}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com