练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列函数中既是奇函数又在区间（0，+∞）上单调递减的是（ ）
    A.y=e﹣x
    B.y=ln（﹣x）
    C.y=x3
    D.

    【答案】D
    【解析】解：由于函数y=e﹣x是减函数，但不是奇函数，故不满足条件． 由于函数y=ln（﹣x）不是奇函数，在（0，+∞）上单调递减，故不满足条件．
    由于函数y=x3是奇函数，且在（0，+∞）上单调递增，故不满足条件．
    由于函数 y= 是奇函数，且在（0，+∞）上单调递减，故满足条件，
    故选D．
    【考点精析】利用函数单调性的判断方法和函数的奇偶性对题目进行判断即可得到答案，需要熟知单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较；偶函数的图象关于y轴对称；奇函数的图象关于原点对称．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=4cosxsin（x+ ）+m（m∈R），当x∈[0， ]时，f（x）的最小值为﹣1．
    （Ⅰ）求m的值；
    （Ⅱ）在△ABC中，已知f（C）=1，AC=4，延长AB至D，使BC=BD，且AD=5，求△ACD的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】解答题。
    （1）已知椭圆C： =1（a＞b＞0）的离心率为 ，以原点为圆心，椭圆的短半轴长为半径的圆与直线 x﹣ y+12=0相切．求椭圆C的方程；
    （2）已知⊙A1：（x+2）2+y2=12和点A2（2，0），求过点A2且与⊙A1相切的动圆圆心P的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】执行下面的程序框图，则输出的k值为（ ）
    A.﹣1
    B.4
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥S﹣ABCD中，底面ABCD是边长为4的菱形，∠ABC=60°，SA⊥平面ABCD，且SA=4，M在棱SA上，且AM=1，N在棱SD上且SN=2ND． （Ⅰ）求证：CN∥面BDM；
    （Ⅱ）求直线SD与平面BDM所成的角的正弦值．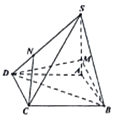

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】集合M的若干个子集的集合称为集合M的一个子集族．对于集合{1，2，3…n}的一个子集族D满足如下条件：若A∈D，BA，则B∈D，则称子集族D是“向下封闭”的． （Ⅰ）写出一个含有集合{1，2}的“向下封闭”的子集族D并计算此时 的值（其中|A|表示集合A中元素的个数，约定||=0； 表示对子集族D中所有成员A求和）；
    （Ⅱ）D是集合{1，2，3…n}的任一“向下封闭的”子集族，对A∈D，记k=max|A|， （其中max表示最大值），
    （ⅰ）求f（2）；
    （ⅱ）若k是偶数，求f（k）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的几何体中，四边形ABCD为正方形，四边形ABEF为直角梯形，且AF∥BE，AB⊥BE，平面ABCD∩平面ABEF=AB，AB=BE=2AF=2． （Ⅰ）求证：AC∥平面DEF；
    （Ⅱ）若二面角D﹣AB﹣E为直二面角，
    （ i）求直线AC与平面CDE所成角的大小；
    （ ii）棱DE上是否存在点P，使得BP⊥平面DEF？若存在，求出 的值；若不存在，请说明理由．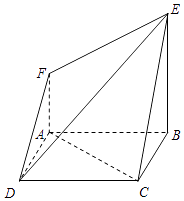

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设f（x）=|ax﹣1|． （Ⅰ）若f（x）≤2的解集为[﹣6，2]，求实数a的值；
    （Ⅱ）当a=2时，若存在x∈R，使得不等式f（2x+1）﹣f（x﹣1）≤7﹣3m成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 （x∈R）．
    （Ⅰ）求函数f（x）的最小正周期及单调递减区间；
    （Ⅱ）若 ，求f（x）的值域．

    查看答案和解析>>

    同步练习册答案