练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    观察下列等式：

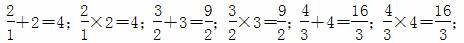    …，根据这些等式反映的结果，可以得出一个关于自然数n的等式，这个等式可以表示为______________________．


    ＋(n＋1)＝×(n＋1)(n∈N*)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


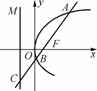
    如图，过抛物线y2＝2px(p>0)的焦点F的直线l交抛物线于点A、B，交其准线于点C.若|BC|＝2|BF|，且|AF|＝3，则此抛物线的方程为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


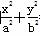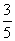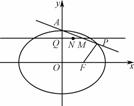
     已知椭圆＝1(a>b>0)的离心率为，且过点P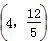，A为上顶点，F为右焦点．点Q(0，t)是线段OA(除端点外)上的一个动点，过Q作平行于x轴的直线交直线AP于点M，以QM为直径的圆的圆心为N.

    (1) 求椭圆方程；

    (2) 若圆N与x轴相切，求圆N的方程；

    (3) 设点R为圆N上的动点，点R到直线PF的最大距离为d，求d的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     若双曲线＝1的离心率e＝2，则m＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    根据下列条件，求双曲线方程．

    (1) 与双曲线＝1有共同的渐近线，且过点(－3，2)；

    (2) 与双曲线＝1有公共焦点，且过点(3，2)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆具有性质：若M、N是椭圆C上关于原点对称的两个点，点P为椭圆上任意一点，当直线PM、PN的斜率都存在，并记为kPM、kPN，那么kPM与kPN之积是与点P位置无关的定值．试对双曲线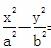＝1写出具有类似特性的性质，并加以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f0(x)＝1－x2，f1(x)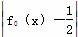＝，fn(x)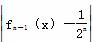＝，(n≥1，n≥N)，则方程f1(x)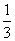＝有________个实数根，方程fn(x)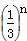＝有________个实数根．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义：如果对任意一个三角形，只要它的三边长a，b，c都在函数f(x)的定义域内，就有f(a)，f(b)，f(c)也是某个三角形的三边长，则称f(x)为“保三角形函数”．若函数h(x)＝lnx (x∈［M，＋∞))是保三角形函数，求M的最小值为                 。

    查看答案和解析>>

    同步练习册答案