练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知数列{an}中,a1=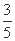,an=2-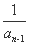(n≥2,n∈N*),数列{bn}满足bn=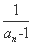(n∈N*).

    (1) 求证:数列{bn}是等差数列;

    (2) 求数列{an}中的最大项和最小项,并说明理由.


     (1) 因为an=2-(n≥2,n∈N*),bn=,

    所以-bn=-

    =-

    =-=1.

    又b1==-,所以数列{bn}是以-为首项、1为公差的等差数列.

    (2) 由(1)知bn=n-,则an=1+=1+,

    设f(x)=1+,则f(x)在区间和上为减函数.

    故当n=3时,an取得最小值-1;当n=4时,an取得最大值3.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图,在区间(0,1]上给定曲线    确定t的值，使S1与S2之和最小。

     


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某车间分批生产某种产品,每批的生产准备费用为800元.若每批生产x件,则平均仓储时间为天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,则每批应生产产品多少件?

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个袋中装有6个形状、大小完全相同的小球,球的编号分别为1,1,1, 2,2,3,现从袋中一次随机抽取3个球.

    (1) 若有放回地抽取3次,求恰有两次抽到编号为3的小球的概率;

    (2) 记球的最大编号为X,求随机变量X的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设等差数列{an}的前n项和为Sn,a2,a4是方程x2-x-2=0的两个根,S5=　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知i与j为互相垂直的单位向量,a=i-2j,b=i+λj,且a与b的夹角为锐角,则实数λ的取值范围是　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,在等腰直角三角形ABC中,AC=BC=1,点M,N分别是AB与BC的中点,点P是△ABC内(包括边界)的一点,求·的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,已知AD=5,DB=8,AO=3,求圆O的半径OC的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点A(0,0),B(2,0),C(2,2)在矩阵M=对应的变换作用下得到的对应点分别为A'(0,0),B'(,1),C'(0,2),求矩阵M.

    查看答案和解析>>

    同步练习册答案