
分析 (Ⅰ)分2步进行分析:1、甲必须站在中间,分析可得这个人只有1种站法,2、将剩余的6个人将全排列,安排在其他6个位置,由分步计数原理计算可得答案;
(Ⅱ)(Ⅲ)先安排甲乙、再安排剩余的5个人;
(Ⅳ)分2步进行分析:1、由于甲乙必须排在一起,用捆绑法将将甲乙看成一个整体,考虑甲乙之间的顺序,2、将这个整体与其他5人进行全排列,由分步计数原理计算可得答案.
解答 解:(Ⅰ)根据题意,甲必须站在中间,则甲只有1种站法,将剩余的6个人将全排列,安排在其他6个位置,有$A_6^6=720$=720种情况,
则甲必须站在中间的排法有1×720=720种;
(Ⅱ)甲乙必须站在两端,先安排甲乙、再安排剩余的5个人,有$A_2^2•A_5^5=240$种;
(Ⅲ)甲乙不能站在两端,先安排甲乙、再安排剩余的5个人,有$A_5^2•A_5^5=2400$种;
(Ⅳ)某2人必须排在一起,将这2人看成一个整体,考虑2人之间的顺序,有A22=2种情况,
将这个整体与其他5人进行全排列,有A66=720种情况,
则某2人必须排在一起的排法有2×720=1440种.
点评 本题考查排列、组合的运用,解题的关键正确理解题意的要求,选择相应的方法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 5377 | B. | -5377 | C. | 5375 | D. | -5375 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{9}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
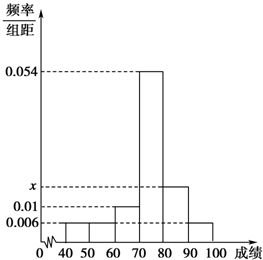 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞\;,\;ln(\sqrt{2}+1)]$ | B. | $[ln(\sqrt{2}-1)\;,\;+∞)$ | ||
| C. | $[ln(\sqrt{2}-1)\;,\;ln(\sqrt{2}+1)]$ | D. | $(-∞\;,\;ln(\sqrt{2}-1)]∪$$[ln(\sqrt{2}+1)\;,\;+∞)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com