
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 通过转化可知问题等价于函数y=1-(x-1)2的图象与y=a(ex-1+$\frac{1}{{e}^{x-1}}$)的图象只有一个交点求a的值.分a=0、a<0、a>0三种情况,结合函数的单调性分析可得结论.
解答 解:因为f(x)=x2-2x+a(ex-1+e-x+1)=-1+(x-1)2+a(ex-1+$\frac{1}{{e}^{x-1}}$)=0,
所以函数f(x)有唯一零点等价于方程1-(x-1)2=a(ex-1+$\frac{1}{{e}^{x-1}}$)有唯一解,
等价于函数y=1-(x-1)2的图象与y=a(ex-1+$\frac{1}{{e}^{x-1}}$)的图象只有一个交点.
①当a=0时,f(x)=x2-2x≥-1,此时有两个零点,矛盾;
②当a<0时,由于y=1-(x-1)2在(-∞,1)上递增、在(1,+∞)上递减,
且y=a(ex-1+$\frac{1}{{e}^{x-1}}$)在(-∞,1)上递增、在(1,+∞)上递减,
所以函数y=1-(x-1)2的图象的最高点为A(1,1),y=a(ex-1+$\frac{1}{{e}^{x-1}}$)的图象的最高点为B(1,2a),
由于2a<0<1,此时函数y=1-(x-1)2的图象与y=a(ex-1+$\frac{1}{{e}^{x-1}}$)的图象有两个交点,矛盾;
③当a>0时,由于y=1-(x-1)2在(-∞,1)上递增、在(1,+∞)上递减,
且y=a(ex-1+$\frac{1}{{e}^{x-1}}$)在(-∞,1)上递减、在(1,+∞)上递增,
所以函数y=1-(x-1)2的图象的最高点为A(1,1),y=a(ex-1+$\frac{1}{{e}^{x-1}}$)的图象的最低点为B(1,2a),
由题可知点A与点B重合时满足条件,即2a=1,即a=$\frac{1}{2}$,符合条件;
综上所述,a=$\frac{1}{2}$,
故选:C.
点评 本题考查函数零点的判定定理,考查函数的单调性,考查运算求解能力,考查数形结合能力,考查转化与化归思想,考查分类讨论的思想,注意解题方法的积累,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
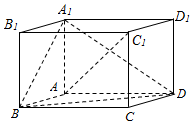 如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=$\sqrt{3}$,∠BAD=120°.
如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=$\sqrt{3}$,∠BAD=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{9}$ | B. | -$\frac{2}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
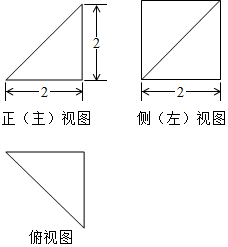
| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 乙可以知道四人的成绩 | B. | 丁可以知道四人的成绩 | ||
| C. | 乙、丁可以知道对方的成绩 | D. | 乙、丁可以知道自己的成绩 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com