
分析 (1)根据抛物线过点P(1,1).代值求出p,即可求出抛物线C的方程,焦点坐标和准线方程;
(2)设过点(0,$\frac{1}{2}$)的直线方程为y=kx+$\frac{1}{2}$,M(x1,y1),N(x2,y2),根据韦达定理得到x1+x2=$\frac{1-k}{{k}^{2}}$,x1x2=$\frac{1}{4{k}^{2}}$,根据中点的定义即可证明.
解答  解:(1)∵y2=2px过点P(1,1),
解:(1)∵y2=2px过点P(1,1),
∴1=2p,
解得p=$\frac{1}{2}$,
∴y2=x,
∴焦点坐标为($\frac{1}{4}$,0),准线为x=-$\frac{1}{4}$,
(2)证明:设过点(0,$\frac{1}{2}$)的直线方程为
y=kx+$\frac{1}{2}$,M(x1,y1),N(x2,y2),
∴直线OP为y=x,直线ON为:y=$\frac{{y}_{2}}{{x}_{2}}$x,
由题意知A(x1,x1),B(x1,$\frac{{x}_{1}{y}_{2}}{{x}_{2}}$),
由$\left\{\begin{array}{l}{y=kx+\frac{1}{2}}\\{{y}^{2}=x}\end{array}\right.$,可得k2x2+(k-1)x+$\frac{1}{4}$=0,
∴x1+x2=$\frac{1-k}{{k}^{2}}$,x1x2=$\frac{1}{4{k}^{2}}$
∴y1+$\frac{{x}_{1}{y}_{2}}{{x}_{2}}$=kx1+$\frac{1}{2}$+$\frac{{x}_{1}(k{x}_{2}+\frac{1}{2})}{{x}_{2}}$=2kx1+$\frac{{x}_{1}+{x}_{2}}{2{x}_{2}}$=2kx1+$\frac{\frac{1-k}{{k}^{2}}}{2×\frac{1}{4{k}^{2}{x}_{1}}}$=2kx1+(1-k)•2x1=2x1,
∴A为线段BM的中点.
点评 本题考查了抛物线的简单性质,以及直线和抛物线的关系,灵活利用韦达定理和中点的定义,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
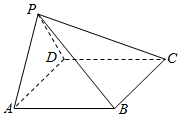 如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{{\sqrt{2}+1}}{2}}]$ | B. | $({-∞,\frac{{\sqrt{2}+1}}{2}}]$ | C. | (-∞,0] | D. | (-∞,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 160 | B. | 163 | C. | 166 | D. | 170 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com