
已知向量 ,
, ,
, ,其中
,其中 为
为 的内角.
的内角.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,且
,且 ,求
,求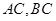 的长.
的长.
科目:高中数学 来源: 题型:解答题
已知关于x的方程:x2-(6+i)x+9+ai=0(a∈R)有实数根b.
(1)求实数a,b的值.
(2)若复数满足|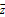 -a-bi|-2|z|=0,求z为何值时,|z|有最小值,并求出|z|的最小值.
-a-bi|-2|z|=0,求z为何值时,|z|有最小值,并求出|z|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知四点A(x,0),B(2x,1),C(2,x),D(6,2x).
(1)求实数x,使两向量 ,
, 共线.
共线.
(2)当两向量 与
与 共线时,A,B,C,D四点是否在同一条直线上?
共线时,A,B,C,D四点是否在同一条直线上?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,设 是单位圆上一点,一个动点从点
是单位圆上一点,一个动点从点 出发,沿圆周按逆时针方向匀速旋转,12秒旋转一周.
出发,沿圆周按逆时针方向匀速旋转,12秒旋转一周. 秒时,动点到达点
秒时,动点到达点 ,
, 秒时动点到达点
秒时动点到达点 .设
.设 ,其纵坐标满足
,其纵坐标满足 .
.
(1)求点 的坐标,并求
的坐标,并求 ;
;
(2)若 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设 为抛物线
为抛物线 (
( )的焦点,
)的焦点,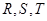 为该抛物线上三点,若
为该抛物线上三点,若 ,且
,且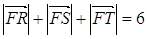
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ) 点的坐标为(
点的坐标为(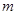 ,
, )其中
)其中 ,过点F作斜率为
,过点F作斜率为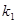 的直线与抛物线交于
的直线与抛物线交于 、
、 两点,
两点, 、
、 两点的横坐标均不为
两点的横坐标均不为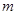 ,连结
,连结 、
、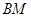 并延长交抛物线于
并延长交抛物线于 、
、 两点,设直线
两点,设直线 的斜率为
的斜率为 .若
.若 ,求
,求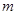 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com