
设 为抛物线
为抛物线 (
( )的焦点,
)的焦点,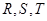 为该抛物线上三点,若
为该抛物线上三点,若 ,且
,且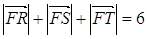
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ) 点的坐标为(
点的坐标为(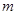 ,
, )其中
)其中 ,过点F作斜率为
,过点F作斜率为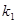 的直线与抛物线交于
的直线与抛物线交于 、
、 两点,
两点, 、
、 两点的横坐标均不为
两点的横坐标均不为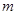 ,连结
,连结 、
、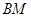 并延长交抛物线于
并延长交抛物线于 、
、 两点,设直线
两点,设直线 的斜率为
的斜率为 .若
.若 ,求
,求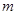 的值.
的值.
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
已知平面向量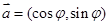 ,
, ,
, ,其中
,其中 ,且函数
,且函数 的图象过点
的图象过点 .
.
(1)求 的值;
的值;
(2)将函数 图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数
图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 在
在 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知数列{an}的前n项和Sn=2n+1-2,等差数列{bn}中,b2=a2,且bn+3+bn-1=2bn+4,(n 2,n
2,n N+),则bn=
N+),则bn=
| A.2n+2 | B.2n | C.n-2 | D.2n-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图,第(1)个图案由1个点组成,第(2)个图案由3个点组成,第(3)个图案由7个点组成,第(4)个图案由13个点组成,第(5)个图案由21个点组成,……,依此类推,根据图案中点的排列规律,第100个图形由多少个点组成( )
| A.9900 | B.9901 | C.9902 | D.9903 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在正项数列{an}中,若a1=1,且对所有n∈N*满足nan+1-(n+1)an=0,则a2014=( )
| A.1011 | B.1012 | C.2013 | D.2014 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com