
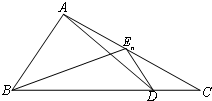
 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中| A. | 2•3n-1-1 | B. | 2n-1 | C. | 3n-2 | D. | 3•2n-1-2 |
分析 利用$\overrightarrow{BD}=3\overrightarrow{DC}$,可得$\overrightarrow{{E}_{n}C}$=$\frac{1}{3}$$\overrightarrow{{E}_{n}B}$+$\frac{2}{3}$$\overrightarrow{{E}_{n}D}$,设m$\overrightarrow{{E}_{n}C}$=$\overrightarrow{{E}_{n}A}$,利用$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,可得$\frac{1}{3}m$=$\frac{1}{4}$an+1,$\frac{2}{3}$m=-(3an+2),即$\frac{1}{4}$an+1=-$\frac{1}{2}$(3an+2),证明{an+1}是以2为首项,3为公比的等比数列,即可得出结论.
解答 解:因为$\overrightarrow{BD}=3\overrightarrow{DC}$,
所以$\overrightarrow{{E}_{n}C}$=$\frac{1}{3}$$\overrightarrow{{E}_{n}B}$+$\frac{2}{3}$$\overrightarrow{{E}_{n}D}$,
设m$\overrightarrow{{E}_{n}C}$=$\overrightarrow{{E}_{n}A}$,则
因为$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,
所以$\frac{1}{3}m$=$\frac{1}{4}$an+1,$\frac{2}{3}$m=-(3an+2),
所以$\frac{1}{4}$an+1=-$\frac{1}{2}$(3an+2),
所以an+1+1=3(an+1),
因为a1+1=2,
所以{an+1}是以2为首项,3为公比的等比数列,
所以an+1=2•3n-1,
所以an=2•3n-1-1.
故选:A.
点评 本题考查数列与向量的综合,考查三点共线,考查等比数列的证明,证明{an+1}是以2为首项,3为公比的等比数列是关键.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
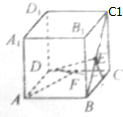 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com