
分析 (Ⅰ)先表示出过点A的切线和过点B的切线,然后两直线联立可求出点N的坐标,即可得到点N在定直线x=-1上;
(Ⅱ)根据$\overrightarrow{{A}{M}}=λ\overrightarrow{{M}{B}}$,可知(1-x1,-y1)=λ(x2-1,y2),进而可联立方程可求得$\frac{1}{{k}^{2}}$的表达式,进而求得范围,最后根据直线MN在y轴的截距,进而可得答案.
解答 解:(I)证明:设直线AB的方程为y=k(x-1),
联立抛物线的方程,可得ky2-y-k=0,
设A(x1,y1),B(x2,y2),可得y1y2=-1,y1+y2=$\frac{1}{k}$,
由点A处的切线的方程为y1y=$\frac{1}{2}$(x+x1),
由点B处的切线的方程为y2y=$\frac{1}{2}$(x+x2),
且y12=x1,y22=x2,
可得y1,y2是关于t的方程t2-2ty+x=0,
即有y1y2=x,
即有x=-1,即为交点N的横坐标,
故点N在一条定直线x=-1上;
(Ⅱ)∵$\overrightarrow{AM}$=λ$\overrightarrow{MB}$,∴(1-x1,-y1)=λ(x2-1,y2),
联立可得$\left\{\begin{array}{l}{-{y}_{1}=λ{y}_{2}}\\{{y}_{1}+{y}_{2}=\frac{1}{k}}\\{{y}_{1}{y}_{2}=-1}\end{array}\right.$,
$\frac{1}{{k}^{2}}$=$\frac{(1-λ)^{2}}{λ}$=$\frac{{λ}^{2}-2λ+1}{λ}$=λ+$\frac{1}{λ}$-2,4≤λ≤9,
∴$\frac{9}{4}$≤$\frac{1}{{k}^{2}}$≤$\frac{64}{9}$即有$\frac{3}{2}$≤$\frac{1}{k}$≤$\frac{8}{3}$或-$\frac{8}{3}$≤$\frac{1}{k}$≤-$\frac{3}{2}$,
由(Ⅰ)可得N(-1,$\frac{{y}_{1}+{y}_{2}}{2}$)即为(-1,$\frac{1}{2k}$),
直线MN:y=-$\frac{1}{4k}$(x-1)在y轴的截距为$\frac{1}{4k}$,
∴直线MN在x轴上截距的取值范围是[$\frac{3}{8}$,$\frac{2}{3}$]∪[-$\frac{2}{3}$,-$\frac{3}{8}$].
点评 本题主要考查了抛物线的应用,涉及了抛物线的性质,向量的计算,不等式等知识,属于中档题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源:2016-2017学年江西上高县二中高二文9月月考数学文试卷(解析版) 题型:选择题
用若干块相同的小正方体搭成一个几何体,从两个角度观察得到的图形如图,则搭成该几何体最少需要的小正方体的块数是( )块?
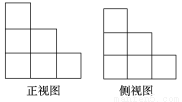
A.8 B.7 C.6 D.5
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川成都石室中学高二理下期中数学试卷(解析版) 题型:选择题
已知函数 ,下列结论中不正确的是( )
,下列结论中不正确的是( )
A.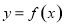 的图象关于点
的图象关于点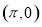 中心对称
中心对称
B.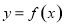 的图象关于直线
的图象关于直线 对称
对称
C.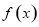 的最大值为
的最大值为
D.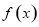 既是奇函数,又是周期函数
既是奇函数,又是周期函数
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({1,\sqrt{2}})$ | B. | $({-\sqrt{2},-1})∪({1,\sqrt{2}})$ | C. | $({-\sqrt{2},\sqrt{2}})$ | D. | $({-\sqrt{2},-1})∪({-1,1})∪({1,\sqrt{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-4y+2=0 | B. | 3x+4y-7=0 | C. | 3x-4y+7=0 | D. | 3x-4y-2=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com