
分析 (1)将点代入抛物线方程,即可求得p的值,求得焦点坐标,则c=1,即a2=b2+1,将点代入椭圆方程,即可求得a和b的值,即可求得椭圆方程;
(2)方法一:设直线l方程,代入抛物线方程,利用韦达定理及向量数量积的坐标运算,b+4k=0,将直线方程代入椭圆方程,由△=0,b2=3+4k2,即可求得b和k的值,即可求得直线方程;
方法二:椭圆的切线方程:$\frac{x{x}_{0}}{4}+\frac{{yy}_{0}}{3}=1$,代入抛物线方程,利用韦达定理及向量数量积的坐标运算,即可求得切点M,代入即可求得直线l的方程.
解答 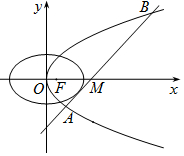 解:(1)由题意可知:将($\frac{2}{3}$,$\frac{{2\sqrt{6}}}{3}}$)代入抛物线方程($\frac{2\sqrt{6}}{3}$)2=$\frac{2}{3}$×2p,解得:2p=4,
解:(1)由题意可知:将($\frac{2}{3}$,$\frac{{2\sqrt{6}}}{3}}$)代入抛物线方程($\frac{2\sqrt{6}}{3}$)2=$\frac{2}{3}$×2p,解得:2p=4,
则抛物线C1:y2=4x,焦点F(1,0),即c=1,a2=b2+1,
将($\frac{2}{3}$,$\frac{{2\sqrt{6}}}{3}}$)代入$\frac{{x}^{2}}{{b}^{2}+1}+\frac{{y}^{2}}{{b}^{2}}=1$,即$\frac{4}{9({b}^{2}+1)}+\frac{8}{3{b}^{2}}=1$,解得:b2=3,a2=4,
椭圆C2的方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
抛物线C1的方程y2=4x,椭圆C2的方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)方法一:设直线AB的方程:y=kx+b,A(x1,y1),B(x2,y2),
$\left\{\begin{array}{l}{y=kx+b}\\{{y}^{2}=4x}\end{array}\right.$,整理得:k2x2+(2kb-4)x+b2=0,
∴x1+x2=-$\frac{2kb-4}{{k}^{2}}$,x1x2=$\frac{{b}^{2}}{{k}^{2}}$,
∴y1y2=(kx1+b)(kx2+b)=k2x1x2+kb(x1+x2)+b2=$\frac{4b}{k}$,
由OA⊥OB,则$\overrightarrow{OA}$+$\overrightarrow{OB}$=0,即x1x2+y1y2=0,即$\frac{{b}^{2}}{{k}^{2}}$+$\frac{4b}{k}$=0,整理得:b+4k=0,①
由$\left\{\begin{array}{l}{y=kx+b}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,整理得:(3+4k2)x2+8kbx+4b2-12=0,
△=(8kb)2-4(3+4k2)(4b2-12)=0,即b2=3+4k2,②
由①②解得:k=±$\frac{1}{2}$,
则$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$或$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-2}\end{array}\right.$,
∴直线l的方程x+2y-4=0或x-2y-4=0.
方法二:设直线AB与椭圆相切于M(x0,y0),A(x1,y1),B(x2,y2),
则椭圆的切线方程:$\frac{x{x}_{0}}{4}+\frac{{yy}_{0}}{3}=1$,
$\left\{\begin{array}{l}{\frac{x{x}_{0}}{4}+\frac{y{y}_{0}}{3}=1}\\{{y}^{2}=4x}\end{array}\right.$,整理得:3x0y2+16y0y-48=0,
则y1+y2=-$\frac{16{y}_{0}}{3{x}_{0}}$,y1y2=-$\frac{16}{{x}_{0}}$,
则x1x2=$\frac{1}{16}$y12y22=$\frac{16}{{x}_{0}^{2}}$,
由OA⊥OB,则$\overrightarrow{OA}$+$\overrightarrow{OB}$=0,即x1x2+y1y2=0,-$\frac{16}{{x}_{0}}$+$\frac{16}{{x}_{0}^{2}}$=0,
解得:x0=1,则y0=±$\frac{3}{2}$,
∴直线l的方程:$\frac{x}{4}+\frac{y}{2}=1$或$\frac{x}{4}-\frac{y}{2}=1$,
直线l的方程x+2y-4=0或x-2y-4=0.
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆及抛物线的位置关系,韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (1,3] | B. | [3,+∞) | C. | (1,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8日 | B. | 9日 | C. | 12日 | D. | 16日 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 测试指标 | [70,76] | [76,82] | [82,88] | [88,94] | [94,100] |
| 装置甲 | 8 | 12 | 40 | 32 | 8 |
| 装置乙 | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | {0,1,2} | C. | (-1,2) | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
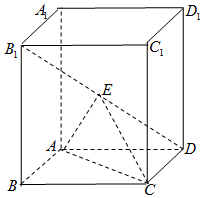 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com