
���� ��I���������C����ͨ���̺ͽ������꣬��ֱ��l�IJ������̴�������C����ͨ�������ø���ϵ���Ĺ�ϵ�Ͳ����ļ�������ó���
��II������εĶ�������Ϊ$��2\sqrt{3}cos�ȣ�2sin�ȣ�$��$��0���ȣ�\frac{��}{2}��$���ɶԳ��Կɵ���ԲC���ڽӾ��ε��ܳ�������˺��������ֵ��
��� �⣺��I�� ��F�ļ�����Ϊ$��2\sqrt{2}���У�$����ֱ������Ϊ$��-2\sqrt{2}��0��$��$\left\{\begin{array}{l}-2\sqrt{2}=m+\frac{{\sqrt{2}}}{2}t\\ 0=\frac{{\sqrt{2}}}{2}t\end{array}\right.$����$m=-2\sqrt{2}$
����C�ļ����귽��Ϊ��2cos2��+3��2sin2��=12��
����ֱ�����귽��Ϊx2+3y2=12-------------------��3�֣�
��ֱ��AB�IJ���������$\left\{\begin{array}{l}x=-2\sqrt{2}+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$��tΪ��������������Cֱ�����귽����
�ɵ�t2-2t-2=0
����|FA|•|FB|=2----------------------------��6�֣�
��������ԲC���ڽӾ����ڵ�һ���Ķ���Ϊ$��2\sqrt{3}cos�ȣ�2sin�ȣ�$��$��0���ȣ�\frac{��}{2}��$
�ɶԳ��Կɵ���ԲC���ڽӾ��ε��ܳ�Ϊ$8\sqrt{3}cos��+8sin��$=$16sin����+\frac{��}{3}��$------------��9�֣�
��$��+\frac{��}{3}=\frac{��}{2}$ʱ����$��=\frac{��}{6}$ʱ��ԲC���ڽӾ��ε��ܳ�ȡ�����ֵ16��---------��10�֣�
���� ���⿼���˲������̣������귽������ͨ���̵�ת������������ֵ���������̵ļ������壬�����е��⣮


 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{4}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{4}{5}$ | D�� | $\frac{7}{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD-A1B1C1D1�У�AA1�͵���ABCD������ABCDΪֱ�����Σ�����AB��CD��AB��AD��AB=AC=2CD=4��AA1=3����AC��ƽ��ֱ���A1B1��B1C1����E1��F1����E1ΪA1B1���е㣮
��ͼ��������ABCD-A1B1C1D1�У�AA1�͵���ABCD������ABCDΪֱ�����Σ�����AB��CD��AB��AD��AB=AC=2CD=4��AA1=3����AC��ƽ��ֱ���A1B1��B1C1����E1��F1����E1ΪA1B1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
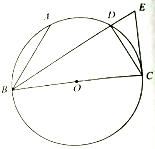 ��ͼ��BC�ǡ�O��ֱ����EC���O������C��AB�ǡ�O���ң�D��$\widehat{AC}$���е㣬BD���ӳ�����CE����E��
��ͼ��BC�ǡ�O��ֱ����EC���O������C��AB�ǡ�O���ң�D��$\widehat{AC}$���е㣬BD���ӳ�����CE����E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
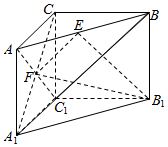 ������ABC-A1B1C1������AA1����ABC��AC1����CBA1��AC1��A1C=F��
������ABC-A1B1C1�У�����AA1����ABC��AC1����CBA1��AC1��A1C=F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
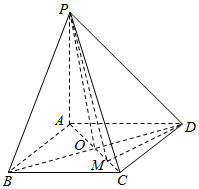 ��֪����P-ABCD�У�PA��ƽ��ABCD������ABCD�DZ߳�Ϊa�����Σ���BAD=120�㣬PA=b��
��֪����P-ABCD�У�PA��ƽ��ABCD������ABCD�DZ߳�Ϊa�����Σ���BAD=120�㣬PA=b���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
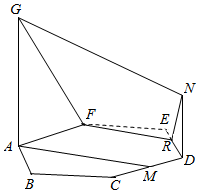 ��ͼ����֪ABCDEF���������Σ�GA��ND����ֱ��ƽ��ABCDEF��ƽ��FGN���߶�DE�ڵ�R����M��CD���е㣬AB=DN=1��AG=2��
��ͼ����֪ABCDEF���������Σ�GA��ND����ֱ��ƽ��ABCDEF��ƽ��FGN���߶�DE�ڵ�R����M��CD���е㣬AB=DN=1��AG=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
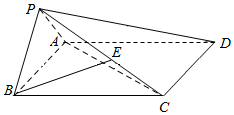 ��ͼ��������P-ABCD�У�����PAB�͵���ABCD������ABCD�DZ߳�Ϊ2�������Σ�PA=PB��EΪPC�ϵĵ㣬��BE��ƽ��PAC��
��ͼ��������P-ABCD�У�����PAB�͵���ABCD������ABCD�DZ߳�Ϊ2�������Σ�PA=PB��EΪPC�ϵĵ㣬��BE��ƽ��PAC���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com