
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
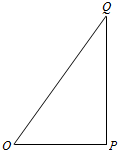 如图,O,P,Q三地有直道相通,OP=3千米,PQ=4千米,OQ=5千米,现甲、乙两警员同时从O地出发匀速前往Q地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是OQ,速度为5千米/小时,乙的路线是OPQ,速度为8千米/小时,乙到达Q地后在原地等待.设t=t1时乙到达P地,t=t2时乙到达Q地.
如图,O,P,Q三地有直道相通,OP=3千米,PQ=4千米,OQ=5千米,现甲、乙两警员同时从O地出发匀速前往Q地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是OQ,速度为5千米/小时,乙的路线是OPQ,速度为8千米/小时,乙到达Q地后在原地等待.设t=t1时乙到达P地,t=t2时乙到达Q地.查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:解答题
已知椭圆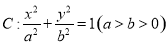 的左、右焦点分别为
的左、右焦点分别为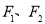 ,椭圆
,椭圆 过点
过点 ,直线
,直线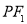 交
交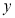 轴于
轴于 ,且
,且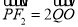 ,
,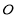 为坐标原点.
为坐标原点.
(1)求椭圆 的方程;
的方程;
(2)设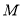 是椭圆
是椭圆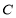 的上顶点,过点
的上顶点,过点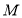 分别作直线
分别作直线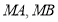 交椭圆
交椭圆 于
于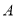 ,
,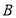 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线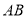 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:选择题
将函数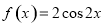 的图象向右平移
的图象向右平移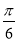 个单位后得到函数
个单位后得到函数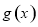 的图象.若函数
的图象.若函数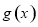 在区间
在区间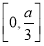 和
和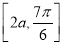 上均单调递增,则实数
上均单调递增,则实数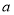 的取值范围是( )
的取值范围是( )
A. B.
B.
C.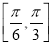 D.
D.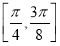
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 |
| y | 20 | 30 | 50 | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com