
分析 ①根据奇函数的定义判断即可;
②根据余弦函数图象的性质判断,对称轴过函数的最值点;
③根据正弦函数图象求解即可;
④函数可化为$f(x)=\frac{cosx+3}{cosx}$=1+$\frac{3}{cosx}$,根据定义域求出函数的值域即可.
解答 解:①函数$f(x)=sin(2x-\frac{π}{3})$,显然f(-x)≠f(x),不是奇函数,故错误;
②f(-$\frac{π}{3}$)=-1,$f(x)=cos(2x-\frac{π}{3})$的一条对称轴方程为$x=-\frac{π}{3}$,故正确;
③函数$f(x)=\sqrt{2}sin(2x+\frac{π}{4})$,$x∈[0,\frac{π}{2}]$,2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{5π}{4}$],则f(x)的值域为[-1,$\sqrt{2}$],故错误;
④函数$f(x)=\frac{cosx+3}{cosx}$=1+$\frac{3}{cosx}$,$x∈(-\frac{π}{2},\frac{π}{2})$,f(x)≥4,有最小值,无最大值,故正确.
故答案为②④.
点评 本题考查了函数的奇偶性,三角函数图象的性质和函数值域的求法.属于基础题型,应熟练掌握.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -23 | B. | 23 | C. | 13 | D. | -13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
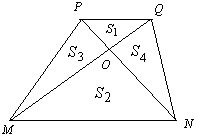 如图,在梯形PMNQ中,PQ∥MN,对角线PN和MQ相交于点O,并把梯形分成四部分,记这四部分的面积分别为S1,S2,S3,S4.试判断S1+S2和S3+S4的大小关系,并证明你的结论.
如图,在梯形PMNQ中,PQ∥MN,对角线PN和MQ相交于点O,并把梯形分成四部分,记这四部分的面积分别为S1,S2,S3,S4.试判断S1+S2和S3+S4的大小关系,并证明你的结论.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A=B | B. | B=C | C. | A=C | D. | A=D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com