
【题目】已知椭圆C:![]() (
(![]() )的两焦点与短轴两端点围成面积为12的正方形.
)的两焦点与短轴两端点围成面积为12的正方形.
(1)求椭圆C的标准方程;
(2)我们称圆心在椭圆上运动,半径为![]() 的圆是椭圆的“卫星圆”.过原点O作椭圆C的“卫星圆”的两条切线,分别交椭圆C于A、B两点,若直线
的圆是椭圆的“卫星圆”.过原点O作椭圆C的“卫星圆”的两条切线,分别交椭圆C于A、B两点,若直线![]() 、
、![]() 的斜率为
的斜率为![]() 、
、![]() ,当
,当![]() 时,求此时“卫星圆”的个数.
时,求此时“卫星圆”的个数.
【答案】(1)![]() ;(2)8个.
;(2)8个.
【解析】
(1)由条件可得![]() ,解出来即可;
,解出来即可;
(2) 设“卫星圆”的圆心为![]() ,由定义可得“卫星圆”的标准方程为
,由定义可得“卫星圆”的标准方程为![]() ,求其圆心到直线
,求其圆心到直线![]() ,直线
,直线![]() 的距离,整理可转化为
的距离,整理可转化为![]() 、
、![]() 是方程
是方程![]() 的两个不相等的实数根,则
的两个不相等的实数根,则![]() ,再加上
,再加上![]() ,
,![]() ,解方程即可.
,解方程即可.
(1)∵椭圆C的两焦点与短轴两端点围成面积为12的正方形,
∴由椭圆的定义和正方形的性质,可得![]() ,
,
解得![]() .
.
又![]()
∴椭圆C的标准方程为![]() .
.
(2)设“卫星圆”的圆心为![]() .
.
由“卫星圆”的定义,可得“卫星圆”的半径为![]() .
.
∴“卫星圆”的标准方程为![]() .
.
∵直线![]() :
:![]() 与“卫星圆”相切,
与“卫星圆”相切,
则由点到直线的距离公式可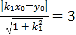 ,
,
化简得![]() .
.
同理可得![]() .
.
∴![]() 、
、![]() 是方程
是方程![]() 的两个不相等的实数根,
的两个不相等的实数根,
∴![]() ,由
,由![]() ,得
,得![]() ,
,
将![]() 代入得
代入得![]() ,
,![]() .
.
又∵“卫星圆”的圆心![]() 在椭圆C上,
在椭圆C上,
∴代入椭圆方程![]() 中,可得
中,可得![]() .
.
解得![]() ,
,
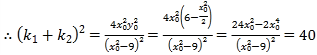 .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
∴满足条件的点![]() 共8个,
共8个,
∴这样“卫星圆”存在8个.


科目:高中数学 来源: 题型:
【题目】移动支付(支付宝及微信支付)已经渐渐成为人们购物消费的一种支付方式,为调查市民使用移动支付的年龄结构,随机对100位市民做问卷调查得到![]() 列联表如下:
列联表如下:
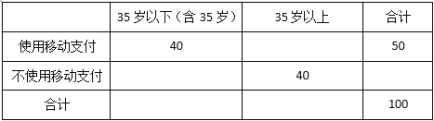
(1)将上![]() 列联表补充完整,并请说明在犯错误的概率不超过0.10的前提下,认为支付方式与年龄是否有关?
列联表补充完整,并请说明在犯错误的概率不超过0.10的前提下,认为支付方式与年龄是否有关?
(2)在使用移动支付的人群中采用分层抽样的方式抽取10人做进一步的问卷调查,从这10人随机中选出3人颁发参与奖励,设年龄都低于35岁(含35岁)的人数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.

(参考公式: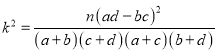 (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 的左焦点为
的左焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() 使得直线
使得直线![]() 的斜率互为相反数?若存在,求出定点
的斜率互为相反数?若存在,求出定点![]() 的坐标;若不存在,也请说明理由.
的坐标;若不存在,也请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲同学参加化学竞赛初赛,考试分为笔试、口试、实验三个项目,各单项通过考试的概率依次为![]() 、
、![]() 、
、![]() ,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
(Ⅰ)若规定总分不低于8分即可进入复赛,求甲同学进入复赛的概率;
(Ⅱ)记三个项目中通过考试的个数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上一点
上一点![]() 与椭圆右焦点的连线垂直于
与椭圆右焦点的连线垂直于![]() 轴,过椭圆
轴,过椭圆![]() 上一点
上一点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(
两点(![]() 均不在坐标轴上),设
均不在坐标轴上),设![]() 为坐标原点,过
为坐标原点,过![]() 的射线
的射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() .
.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)当![]() 为
为![]() 时,若四边形
时,若四边形![]() 的面积为12,试求直线
的面积为12,试求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com