
 ��ͼ����У100������ѧ����6���¿�������ѧ�ɼ���Ƶ�ʷֲ�ֱ��ͼ�����гɼ����������ǣ�[50��60����[60��70����[70��80����[80��90����[90��100]��
��ͼ����У100������ѧ����6���¿�������ѧ�ɼ���Ƶ�ʷֲ�ֱ��ͼ�����гɼ����������ǣ�[50��60����[60��70����[70��80����[80��90����[90��100]��| ������ | [50��60�� | [60��70�� | [70��80�� | [80��90�� |
| x��y | 1��1 | 2��1 | 3��4 | 4��5 |
���� ��1���������Ը��ʵĺ�Ϊ1����������ε������Ϊ1��������ʽ��ϵ�����������ֵΪ��������ֵ�����Ƶ��֮���ĺͣ�
��2���ֱ�������ε�������������������ɼ���[50��90��֮�������Ϊ��
��� �⣺��1��������ã�10����2a+0.02+0.03+0.04��=1�����a=0.005��
��100��ѧ����ѧ�ɼ���ƽ����Ϊ��
55��0.05+65��0.4+75��0.3+85��0.2+95��0.05=73��
��2�������ɼ���[50��60��������Ϊ��100��0.05=5��
�����ɼ���[60��70��������Ϊ��100��0.4��$\frac{1}{2}=20$��
�����ɼ���[70��80��������Ϊ��100��0.3��$\frac{4}{3}=40$��
�����ɼ���[80��90��������Ϊ��100��0.2��$\frac{5}{4}=25$��
���Ե����ɼ���[50��90��֮�������Ϊ��100-5-20-40-25=10��
���� ������Ҫ����Ƶ�ʷֲ�ֱ��ͼ��ƽ���������ѶȲ������ڻ����⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
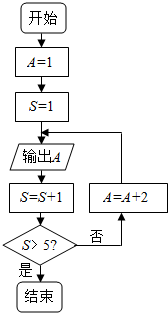
| A�� | 7��9 | B�� | 5��11 | C�� | 7��11 | D�� | 5��9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -6 | B�� | $\frac{3}{2}$ | C�� | 6 | D�� | $\frac{13}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ�㾥Ҷͼ����Ҷ����С�����˳��д���Ҳ�����ݰ���С�����˳��д����ͬ�����ݿ���ֻ��һ�� | |
| B�� | ϵͳ�����ڵ�һ�γ���ʱһ����ü�������� | |
| C�� | �����¼��ĺ��¼���ָ�����¼����������¼� | |
| D�� | �ֲ����ÿ���������������Բ�ͬ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1} | B�� | {2} | C�� | {0��1} | D�� | {1��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��һ�����ǰ�ABC��ABD�ڳ���ͼ��ʾ��ֱ�����D-AB-C��������BD=2AD��BC=AC��������ֱ��DC��AB���ɽǵ�����ֵΪ��������
��һ�����ǰ�ABC��ABD�ڳ���ͼ��ʾ��ֱ�����D-AB-C��������BD=2AD��BC=AC��������ֱ��DC��AB���ɽǵ�����ֵΪ��������| A�� | $\sqrt{3}$ | B�� | $\sqrt{7}$ | C�� | $\frac{{\sqrt{21}}}{7}$ | D�� | $\frac{{\sqrt{21}}}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com