
分析 (1)利用等差数列通项公式和前n项和公式列出方程组,求出首项和公差,由此能求出数列{an}的通项公式.
(2)令${b}_{n}=\frac{1}{{a}_{n}{a}_{n+2}}$=$\frac{4}{(n+1)(n+3)}$=2($\frac{1}{n+1}-\frac{1}{n+3}$),利用裂项求和法能求出数列{$\frac{1}{{{a_n}{a_{n+2}}}}$}的前n项和.
解答 解:(1)在等差数列{an}中设首项为a1,公差为d,
∵a5=3,前3项和S3为$\frac{9}{2}$,
∴$\left\{\begin{array}{l}{{a}_{1}+4d=3}\\{3{a}_{1}+\frac{3×2d}{2}=\frac{9}{2}}\end{array}\right.$,
解得${a}_{1}=1,d=\frac{1}{2}$,
∴an=$\frac{1}{2}(n+1)$.
(2)令${b}_{n}=\frac{1}{{a}_{n}{a}_{n+2}}$=$\frac{4}{(n+1)(n+3)}$=2($\frac{1}{n+1}-\frac{1}{n+3}$),
∴数列{$\frac{1}{{{a_n}{a_{n+2}}}}$}的前n项和:
Tn=2($\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{n+1}-\frac{1}{n+3}$)
=2($\frac{1}{2}+\frac{1}{3}-\frac{1}{n+2}-\frac{1}{n+3}$)
=$\frac{n(5n+13)}{3(n+2)(n+3)}$.
点评 本题考查数列的通项公式及前n项和公式的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{4}$ | B. | x=$\frac{π}{8}$ | C. | x=$\frac{π}{12}$ | D. | x=$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1+$\sqrt{3}$ | C. | $\frac{5}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行 | B. | 垂直 | C. | 相交 | D. | 重合 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
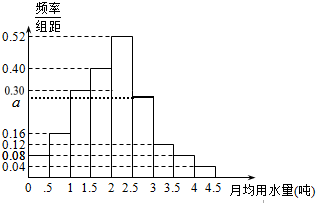 我国是世界上严重缺水的国家,城市缺水尤为突出.某市为了制定合理的节水方案,从该市随机调查了100位居民,获得了他们某月的用水量,整理得到如图的频率分布直方图.
我国是世界上严重缺水的国家,城市缺水尤为突出.某市为了制定合理的节水方案,从该市随机调查了100位居民,获得了他们某月的用水量,整理得到如图的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4π}{3}$ | B. | $\frac{5π}{3}$ | C. | 2π | D. | $\frac{7π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com