
科目:高中数学 来源: 题型:解答题
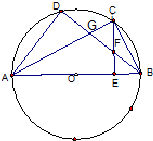 如图,已知AB为圆O的直径,C,D是圆O上的两个点,C是劣弧$\widehat{BD}$的中点,CE⊥AB于E,BD交AC于G,交CE于F.
如图,已知AB为圆O的直径,C,D是圆O上的两个点,C是劣弧$\widehat{BD}$的中点,CE⊥AB于E,BD交AC于G,交CE于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)-f(1)<0 | B. | f(-1)-f(1)>0 | C. | f(-1)+f(1)<0 | D. | f(-1)+f(1)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,x03>x02 | B. | ?x0∉R,x03>x02 | C. | ?x0∈R,x03≤x02 | D. | ?x0∉R,x03≤x02 | ||||
| E. | ?x0∈R,x03≤x02 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
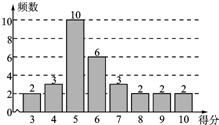 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为me,众数为
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为me,众数为| A. | me=mo | B. | mo<me | C. | me<mo | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com