
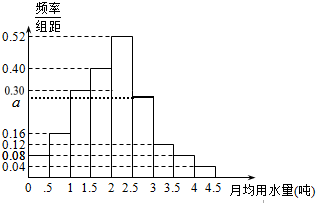
 我国是世界上严重缺水的国家,城市缺水尤为突出.某市为了制定合理的节水方案,从该市随机调查了100位居民,获得了他们某月的用水量,整理得到如图的频率分布直方图.
我国是世界上严重缺水的国家,城市缺水尤为突出.某市为了制定合理的节水方案,从该市随机调查了100位居民,获得了他们某月的用水量,整理得到如图的频率分布直方图.分析 (1)由频率分布直方图可知每段内的频率,由此利用频率分布直方图的性质能求出a的值.
(2)先求出不低于3吨的频率,由此能求出月均用水量不低于3吨的人数.
(3)利用频率分布直方图的性质能求出月平均用水量.
解答 解:(1)由频率分布直方图可知每段内的频率:
[0,0.5]:0.04;(0.5,1]:0.08;(1,1.5]:0,15; (1.5,2]:0.22; (2,2.5]:0.25;
(2.5,3]:0.5a;(3,3.5]:0.06;(3.5,4]:0.04;(4.4.5]:0.02,…(2分)
则由0.04+0.08+0.15+0.22+0.25+0.5a+0.06+0.04+0.02=1,
解得a=0.28.…(4分)
(2)∵不低于3吨的频率为0.06+0.04+0.02=0.12,…(6分)
∴月均用水量不低于3吨的人数为500×0.12=60万.…(8分)
(3)月平均用水量为:
0.04×0.25+0.08×0.75+0.15×1.25+0.22×1.75+0.25×2.25+0.14×2.75+0.06×3,25+0.04×3.75+0.02×4.25…(10分)
=2.02(吨)
∴人月平均用水量为2.02吨.…12分
点评 本题考查实数值的求法,考查频数、平均数的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)-f(1)<0 | B. | f(-1)-f(1)>0 | C. | f(-1)+f(1)<0 | D. | f(-1)+f(1)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
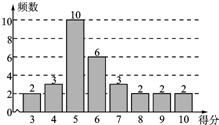 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为me,众数为
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为me,众数为| A. | me=mo | B. | mo<me | C. | me<mo | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com