
【题目】在![]() 中,内角
中,内角![]() 的对边分别为
的对边分别为![]() ,已知
,已知![]() .
.
(1)求角![]() 的值;
的值;
(2)若![]() ,当
,当![]() 取最小值时,求
取最小值时,求![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:方法一:(Ⅰ)利用正弦定理、诱导公式、两角和的正弦公式化简已知的式子,由内角的范围和特殊角的三角函数值求出角C;(Ⅱ)利用余弦定理列出方程,由条件和完全平方公式化简后,利用基本不等式求出c的最小值,由面积公式求出△ABC的面积;方法二:(Ⅰ)利用余弦定理化简已知的式子得到边的关系,由余弦定理求出cosC的值,由内角的范围和特殊角的三角函数值求出角C;(Ⅱ)利用余弦定理列出方程,结合条件消元后,利用一元二次函数的性质求出c的最小值,由面积公式求出△ABC的面积
试题解析:解法一(1)∵![]() ,∴
,∴![]() ……………………1分
……………………1分
∴![]() ……………2分
……………2分
即 ![]() ……………3分
……………3分
∴![]() 4分
4分
∵![]() ∴
∴ ![]() …………5分
…………5分
又∵![]() 是三角形的内角,∴
是三角形的内角,∴![]() ……6分
……6分
(2)由余弦定理得:![]() …………7分
…………7分
∵ ![]() ,故
,故![]() 8分
8分
∴ ![]() (当且仅当
(当且仅当![]() 时等号成立) ………10分
时等号成立) ………10分
∴![]() 的最小值为2,故
的最小值为2,故![]() ……12分
……12分
解法二:(1)∵![]() ,∴
,∴ ![]() ………1分
………1分
∴ ![]() ,即
,即 ![]() …………3分
…………3分
∴ ![]() …5分
…5分
又∵![]() 是三角形的内角,∴
是三角形的内角,∴![]() 6分
6分
(2)由已知,![]() ,即
,即![]() ,故:
,故:
![]() ……………8分
……………8分
∴ ![]() …………10分
…………10分
∴当![]() 时,
时,![]() 的最小值为2,故
的最小值为2,故![]() …………12分
…………12分


科目:高中数学 来源: 题型:
【题目】国庆假期是实施免收小型客车高速通行费的重大节假日,有一个群名为“天狼星”的自驾游车队,该车队是由31辆身长约为![]() (以
(以![]() 计算)的同一车型组成,行程中经过一个长为2725
计算)的同一车型组成,行程中经过一个长为2725![]() 的隧道(通过隧道的车速不超过
的隧道(通过隧道的车速不超过![]() ),匀速通过该隧道,设车队的速度为
),匀速通过该隧道,设车队的速度为![]() ,根据安全和车流的需要,当
,根据安全和车流的需要,当![]() 时,相邻两车之间保持
时,相邻两车之间保持![]() 的距离;当
的距离;当![]() 时,相邻两车之间保持
时,相邻两车之间保持![]() 的距离,自第一辆车车头进入隧道至第31辆车车尾离开隧道所用的时间
的距离,自第一辆车车头进入隧道至第31辆车车尾离开隧道所用的时间![]() .
.
(1)将![]() 表示成为
表示成为![]() 的函数;
的函数;
(2)求该车队通过隧道时间![]() 的最小值及此时车队的速度.
的最小值及此时车队的速度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() ),且数列
),且数列![]() 是首项为2,公差为2的等差数列.
是首项为2,公差为2的等差数列.
(1)若![]() ,当
,当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2)设![]() ,如果
,如果![]() 中的每一项恒小于它后面的项,求
中的每一项恒小于它后面的项,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如右表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
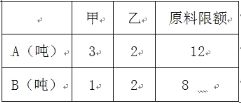
A.12万元 B.16万元
C.17万元 D.18万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个长方体的平面展开图及该长方体的直观图的示意图如图所示.
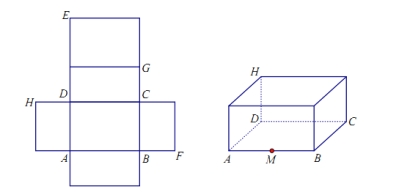
(1)请将字母![]() 标记在长方体相应的顶点处(不需说明理由);
标记在长方体相应的顶点处(不需说明理由);
(2)在长方体中,判断直线![]() 与平面
与平面![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)在长方体中,设![]() 的中点为
的中点为![]() ,且
,且![]() ,
,![]() ,求证:
,求证:
![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
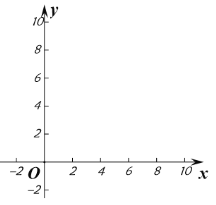
(1)在区间![]() 上画出函数
上画出函数![]() 的图象;
的图象;
(2)设集合![]() ,
,![]() .试判断集合
.试判断集合![]() 和
和![]() 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当![]() 时,求证:在区间
时,求证:在区间![]() 上,
上,![]() 的图象位于函数
的图象位于函数![]() 图象的上方.
图象的上方.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴正半轴上的圆
轴正半轴上的圆![]() 与直线
与直线![]() 相切,与
相切,与![]() 轴交于
轴交于![]() 两点,且
两点,且![]() .
.
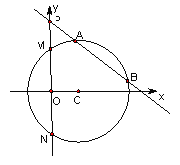
(1)求圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,若设点
,若设点![]() 为
为![]() 的重心,当
的重心,当![]() 的面积为
的面积为![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,四边形
,四边形![]() 为正方形,点
为正方形,点![]() 分别为线段
分别为线段![]() 上的点,
上的点,![]() .
.
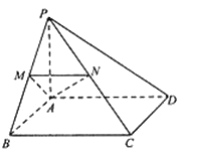
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:当点![]() 不与点
不与点![]() 重合时,
重合时,![]() 平面
平面![]() ;
;
(3)当![]() 时,求点
时,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com