
【题目】已知函数![]()
(1)当![]() 时,求满足
时,求满足![]() 的
的![]() 的取值:
的取值:
(2)若函数![]() 是定义在
是定义在![]() 上的奇函数
上的奇函数
①存在![]() ,不等式
,不等式![]() 有解,求
有解,求![]() 的取值范围;
的取值范围;
②若函数![]() 满足
满足![]() ,若对任意
,若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
【答案】(1)![]() ,(2)①
,(2)①![]() ,②6
,②6
【解析】分析:(1)根据![]()
![]() ,可将方程
,可将方程![]()
![]() 转化为一元二次方程:
转化为一元二次方程:![]() ,再根据指数函数范围可得
,再根据指数函数范围可得![]() ,解得
,解得![]() ,(2)①先根据函数奇偶性确定
,(2)①先根据函数奇偶性确定![]() 值:
值:![]() ,再利用单调性定义确定其单调性;在
,再利用单调性定义确定其单调性;在![]() 上递调,最后根据单调性转化不等式
上递调,最后根据单调性转化不等式![]() 为
为![]() ,即
,即![]() 在
在![]() 时有解,根据判别式大于零可得
时有解,根据判别式大于零可得![]() 的取值范围。②先求函数
的取值范围。②先求函数![]() :
:![]() ,则
,则![]() ,因此不等式可转化为一元二次不等式,并将其变量分离得:
,因此不等式可转化为一元二次不等式,并将其变量分离得:![]() 的最小值,其中
的最小值,其中![]() ,利用基本不等式求最值得
,利用基本不等式求最值得![]()
详解:(1)由题意,![]() ,化简得
,化简得![]()
解得![]() (舍)或
(舍)或![]() ,
,
所以![]()
(2)因为![]() 是奇函数,所以
是奇函数,所以![]() ,所以
,所以![]()
化简并变形得:![]()
要使上式对任意![]() 的成立,则
的成立,则![]() 或
或![]()
解得:![]() 或
或![]() ,因为
,因为![]() 的定义域是
的定义域是![]() ,所以
,所以![]() 舍去
舍去
所以![]() ,所以
,所以![]()
①![]()
对任意![]() ,
,![]() 有:
有:
![]()
![]()
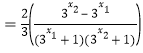
因为![]() ,所以
,所以![]() ,所以
,所以![]()
因此![]() 在
在![]() 上递减
上递减
因为![]() ,所以
,所以![]()
即![]() 在
在![]() 时有解,所以
时有解,所以![]() ,解得
,解得![]()
所以![]() 的取值范围为
的取值范围为![]()
②因为![]() ,所以
,所以![]()
即![]()
所以![]()
不等式![]() 恒成立,
恒成立,
即![]()
即![]() 恒成立,
恒成立,
令![]() ,
,![]() ,则
,则![]() 在
在![]() 时恒成立
时恒成立
令![]() ,
,![]()
![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减
上单调递减
![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增
上单调递增
所以![]() ,所以
,所以![]()
所以,实数![]() 的最大值是6.
的最大值是6.


科目:高中数学 来源: 题型:
【题目】自“钓鱼岛事件”以来,中日关系日趋紧张并不断升级.为了积极响应“保钓行动”,某学校举办了一场“保钓知识大赛”,共分两组.其中甲组得满分的有1个女生和3个男生,乙组得满分的有2个女生和4个男生.现从得满分的同学中,每组各任选1个同学,作为“保钓行动代言人”.
(1)求选出的2个同学中恰有1个女生的概率;
(2)设X为选出的2个同学中女生的个数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 数列{bn},{cn}满足 (n+1)bn=an+1﹣ ![]() ,(n+2)cn=
,(n+2)cn= ![]() ﹣
﹣ ![]() ,其中n∈N*.
,其中n∈N*.
(1)若数列{an}是公差为2的等差数列,求数列{cn}的通项公式;
(2)若存在实数λ,使得对一切n∈N*,有bn≤λ≤cn , 求证:数列{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某舆情机构为了解人们对某事件的关注度,随机抽取了![]() 人进行调查,其中女性中对该事件关注的占
人进行调查,其中女性中对该事件关注的占![]() ,而男性有
,而男性有![]() 人表示对该事件没有关注.
人表示对该事件没有关注.
关注 | 没关注 | 合计 | |
男 |
| ||
女 | |||
合计 |
(1)根据以上数据补全![]() 列联表;
列联表;
(2)能否有![]() 的把握认为“对事件是否关注与性别有关”?
的把握认为“对事件是否关注与性别有关”?
(3)已知在被调查的女性中有![]() 名大学生,这其中有
名大学生,这其中有![]() 名对此事关注.现在从这
名对此事关注.现在从这![]() 名女大学生中随机抽取
名女大学生中随机抽取![]() 人,求至少有
人,求至少有![]() 人对此事关注的概率.
人对此事关注的概率.
附表:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有 ![]() (n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:
(n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵: 
设Mk是第k行中的最大数,其中1≤k≤n,k∈N*.记M1<M2<…<Mn的概率为pn .
(1)求p2的值;
(2)证明:pn> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(江苏省南京师大附中2018届高三高考考前模拟考试数学试题)已知函数f(x)=lnx-ax+a,a∈R.
(1)若a=1,求函数f(x)的极值;
(2)若函数f(x)有两个零点,求a的范围;
(3)对于曲线y=f(x)上的两个不同的点P(x1,f(x1)),Q(x2,f(x2)),记直线PQ的斜率为k,若y=f(x)的导函数为f ′(x),证明:f ′(![]() )<k.
)<k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=ex﹣ax﹣1,其中e为自然对数的底数,a∈R.
(1)若a=e,函数g (x)=(2﹣e)x. ①求函数h(x)=f (x)﹣g (x)的单调区间;
②若函数F(x)= ![]() 的值域为R,求实数m的取值范围;
的值域为R,求实数m的取值范围;
(2)若存在实数x1 , x2∈[0,2],使得f(x1)=f(x2),且|x1﹣x2|≥1,求证:e﹣1≤a≤e2﹣e.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,圆C:
,圆C: ![]() ,
,
(1)过点![]() 向圆C引切线l,求切线l的方程;
向圆C引切线l,求切线l的方程;
(2)过点A作直线![]() 交圆C于P,Q,且
交圆C于P,Q,且![]() ,求直线
,求直线![]() 的斜率k;
的斜率k;
(3)定点M,N在直线![]() 上,对于圆C上任意一点R都满足
上,对于圆C上任意一点R都满足![]() ,试求M,N两点的坐标.
,试求M,N两点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com